题目内容
(1)计算:
-
+(
)2-
(2)已知关于x的一元二次方程(a+1)x2-x+a2-3a-3=0有一根是1.
①求a的值;
②求方程的另一根.
| 1 |
| 2 |
| 24 |
| (-3)2 |
| 3 |
| 54 |
(2)已知关于x的一元二次方程(a+1)x2-x+a2-3a-3=0有一根是1.
①求a的值;
②求方程的另一根.
考点:实数的运算,一元二次方程的解,根与系数的关系
专题:计算题
分析:(1)原式利用二次根式的性质化简,计算即可得到结果;
(2)①把x=1代入方程计算即可求出a的值;
②由a的值确定出方程,求出方程的另一根即可.
(2)①把x=1代入方程计算即可求出a的值;
②由a的值确定出方程,求出方程的另一根即可.
解答:解:(1)原式=
-3+3-3
=-2
;
(2)①把x=1代入方程得:a+1-1+a2-3a-3=0,即a2-2a-3=0,
解得:a=3或a=-1(舍去),
则a=3;
②把a=3代入方程得:4x2-x-3=0,
解得:x=1或x=-
,
则方程的另一根为-
.
| 6 |
| 6 |
| 6 |
(2)①把x=1代入方程得:a+1-1+a2-3a-3=0,即a2-2a-3=0,
解得:a=3或a=-1(舍去),
则a=3;
②把a=3代入方程得:4x2-x-3=0,
解得:x=1或x=-
| 3 |
| 4 |
则方程的另一根为-
| 3 |
| 4 |
点评:此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
下列说法:
①角平分线上的点到这个角两条边的距离相等
②线段的垂直平分线上的点到这条线段的两个端点的距离相等
③三角形三条角平分线的交点到这个三角形三个顶点的距离相等.
④三角形三条角平分线的交点到这个三角形三边的距离相等.
其中正确的结论有( )
①角平分线上的点到这个角两条边的距离相等
②线段的垂直平分线上的点到这条线段的两个端点的距离相等
③三角形三条角平分线的交点到这个三角形三个顶点的距离相等.
④三角形三条角平分线的交点到这个三角形三边的距离相等.
其中正确的结论有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列说法正确的是( )
| A、等腰三角形的两个底角相等 |
| B、顶角相等的两个等腰三角形全等 |
| C、等腰三角形的高、中线、角平分线互相重合 |
| D、等腰三角形一边不可以是另一边的二倍 |
下列各组代数式中,不是同类项的是( )
| A、9与-5 |
| B、-0.5xy2与3x2y |
| C、-3t与200t |
| D、ab2与-8b2a |
下列命题中,是真命题的是( )
| A、无限小数都是无理数 |
| B、|a|>0 |
| C、同角的余角相等 |
| D、有公共顶点且相等的两个角是对顶角 |
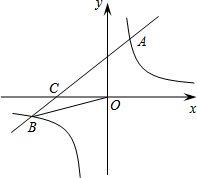 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2= 已知,如图,△ABC≌△DCE≌△FEG,点B、C、E、G在同一直线上,
已知,如图,△ABC≌△DCE≌△FEG,点B、C、E、G在同一直线上, 如图,△ABO≌△CBO,若∠A=85°,∠ABO=35°,则∠BOC的度数为
如图,△ABO≌△CBO,若∠A=85°,∠ABO=35°,则∠BOC的度数为