题目内容
解下列方程
(1)2x2-
=0;
(2)2x2-4x+1=0(配方法)
(3)2(x-3)2=x(x-3);
(4)3y2+5(2y+1)=0 (公式法).
(1)2x2-
| 1 |
| 2 |
(2)2x2-4x+1=0(配方法)
(3)2(x-3)2=x(x-3);
(4)3y2+5(2y+1)=0 (公式法).
考点:解一元二次方程-直接开平方法,解一元二次方程-配方法,解一元二次方程-公式法,解一元二次方程-因式分解法
专题:计算题
分析:(1)方程变形后,利用直接开平方法求出解即可;
(2)方程利用配方法求出解即可;
(3)方程利用因式分解法求出解即可;
(4)方程利用公式法求出解即可.
(2)方程利用配方法求出解即可;
(3)方程利用因式分解法求出解即可;
(4)方程利用公式法求出解即可.
解答:解:(1)方程变形得:x2=
,
开方得:x=±
;
(2)方程变形得:x2-2x=-
,
配方得:x2-2x+1=
,即(x-1)2=
,
开方得:x-1=±
,
解得:x1=1+
,x2=1-
;
(3)方程变形得:2(x-3)2-x(x-3)=0,
分解因式得:(x-3)(2x-6-x)=0,
解得:x1=3,x2=6;
(4)方程整理得:3y2+10y+5=0,
这里a=3,b=10,c=5,
∵△=100-60=40,
∴y=
=
.
| 1 |
| 4 |
开方得:x=±
| 1 |
| 2 |
(2)方程变形得:x2-2x=-
| 1 |
| 2 |
配方得:x2-2x+1=
| 1 |
| 2 |
| 1 |
| 2 |
开方得:x-1=±
| ||
| 2 |
解得:x1=1+
| ||
| 2 |
| ||
| 2 |
(3)方程变形得:2(x-3)2-x(x-3)=0,
分解因式得:(x-3)(2x-6-x)=0,
解得:x1=3,x2=6;
(4)方程整理得:3y2+10y+5=0,
这里a=3,b=10,c=5,
∵△=100-60=40,
∴y=
-10±2
| ||
| 6 |
-5±
| ||
| 3 |
点评:此题考查了解一元二次方程-直接开平方法,熟练掌握平方根定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中,是真命题的是( )
| A、无限小数都是无理数 |
| B、|a|>0 |
| C、同角的余角相等 |
| D、有公共顶点且相等的两个角是对顶角 |
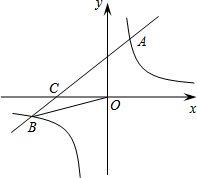 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2= 如图,△ABO≌△CBO,若∠A=85°,∠ABO=35°,则∠BOC的度数为
如图,△ABO≌△CBO,若∠A=85°,∠ABO=35°,则∠BOC的度数为 如图,AB、CD是⊙O的直径,OE⊥AB,OF⊥CD,则∠EOD
如图,AB、CD是⊙O的直径,OE⊥AB,OF⊥CD,则∠EOD