题目内容
 如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为
如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为考点:全等三角形的性质
专题:动点型,分类讨论
分析:由条件分两种情况,当△BPE≌△CQP时,则有BE=PC,由条件可得到关于t的方程,当△BPE≌△CPQ,则有BP=PC,同样可得出t的方程,可求出t的值.
解答:解:
∵AB=20cm,AE=6cm,BC=16cm,
∴BE=14cm,BP=2tcm,PC=(16-2t)cm,
当△BPE≌△CQP时,则有BE=PC,即14=16-2t,解得t=1,
当△BPE≌△CPQ时,则有BP=PC,即2t=16-2t,解得t=4,
故答案为:1或4.
∵AB=20cm,AE=6cm,BC=16cm,
∴BE=14cm,BP=2tcm,PC=(16-2t)cm,
当△BPE≌△CQP时,则有BE=PC,即14=16-2t,解得t=1,
当△BPE≌△CPQ时,则有BP=PC,即2t=16-2t,解得t=4,
故答案为:1或4.
点评:本题主要考查全等三角形的性质,由条件分两种情况得到关于t的方程是解题的关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
下列说法正确的是( )
| A、等腰三角形的两个底角相等 |
| B、顶角相等的两个等腰三角形全等 |
| C、等腰三角形的高、中线、角平分线互相重合 |
| D、等腰三角形一边不可以是另一边的二倍 |
下列各组代数式中,不是同类项的是( )
| A、9与-5 |
| B、-0.5xy2与3x2y |
| C、-3t与200t |
| D、ab2与-8b2a |
下列命题中,是真命题的是( )
| A、无限小数都是无理数 |
| B、|a|>0 |
| C、同角的余角相等 |
| D、有公共顶点且相等的两个角是对顶角 |
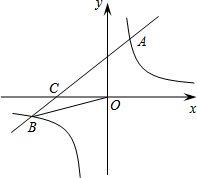 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2= 如图,AB、CD是⊙O的直径,OE⊥AB,OF⊥CD,则∠EOD
如图,AB、CD是⊙O的直径,OE⊥AB,OF⊥CD,则∠EOD