题目内容
如图，在△ABC中，AB=AC，AD平分∠BAC，那么下列结论不一定成立的是（ ）| A、△ABD≌△ACD |
| B、AD是△ABC的高线 |
| C、AD是△ABC的角平分线 |
| D、△ABC是等边三角形 |
考点：等腰三角形的性质
专题：
分析：利用等腰三角形的性质逐项判断即可．
解答：解：
A、在△ABD和△ACD中，
，所以△ABD≌△ACD，所以A正确；
B、因为AB=AC，AD平分∠BAC，所以AD是BC边上的高，所以B正确；
C、由条件可知AD为△ABC的角平分线；
D、由条件无法得出AB=AC=BC，所以△ABC不一定是等边三角形，所以D不正确；
故选D．
A、在△ABD和△ACD中，
|
B、因为AB=AC，AD平分∠BAC，所以AD是BC边上的高，所以B正确；
C、由条件可知AD为△ABC的角平分线；
D、由条件无法得出AB=AC=BC，所以△ABC不一定是等边三角形，所以D不正确；
故选D．
点评：本题主要考查等腰三角形的性质，掌握等腰三角形“三线合一”的性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
在下列长度的各组线段中，能构成直角三角形的是（ ）
| A、3，5，9 | ||||||
B、1，
| ||||||
| C、4，6，8 | ||||||
D、
|
下列说法正确的是（ ）
| A、等腰三角形的两个底角相等 |
| B、顶角相等的两个等腰三角形全等 |
| C、等腰三角形的高、中线、角平分线互相重合 |
| D、等腰三角形一边不可以是另一边的二倍 |
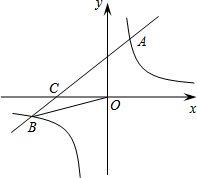如图，在平面直角坐标系xOy中，一次函数y1=ax+b（a≠0）的图象与反比例函数y2=