题目内容
2.已知a+b=3,ab=-2,求下列代数式的值.(1)(a-b)2=17.(2)a2+b2+ab=11.
分析 (1)原式利用完全平方公式化简,将已知等式代入计算即可求出值;
(2)把a+b=3两边平方,利用完全平方公式化简,将ab=-2代入计算求出a2+b2的值,即可确定出所求.
解答 解:(1)∵a+b=3,ab=-2,
∴(a-b)2=(a+b)2-4ab=9+8=17;
(2)∵a+b=3,ab=-2,
∴(a+b)2=a2+b2+2ab=9,即a2+b2-4=9,
解得:a2+b2=13,
则原式=13-2=11.
故答案为:(1)17;(2)11
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 任何非负数都有两个平方根 | B. | 一个正数的平方根仍然是正数 | ||
| C. | 只有正数才有平方根 | D. | 负数没有平方根 |
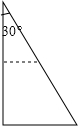 如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是8或4+2$\sqrt{3}$.
如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是8或4+2$\sqrt{3}$.