题目内容
5. 如图,建筑物AB后有一座假山,其坡度为i=1:$\sqrt{3}$,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,建筑物AB后有一座假山,其坡度为i=1:$\sqrt{3}$,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
分析 首先过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,再利用坡度的定义以及勾股定理得出EF、FC的长,求出AB的长即可.
解答  解:过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,
解:过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,
∵建筑物AB后有一座假山,其坡度为i=1:$\sqrt{3}$,
∴设EF=x,则FC=$\sqrt{3}$x,
∵CE=20米,
∴x2+($\sqrt{3}$x)2=400,
解得:x=10,
则FC=10$\sqrt{3}$m,
∵BC=25m,∴BF=NE=(25+10$\sqrt{3}$)m,
∴AB=AN+BN=NE+EF=10+25+10$\sqrt{3}$=(35+10$\sqrt{3}$)m,
答:建筑物AB的高为(35+10$\sqrt{3}$)m.
点评 本题考查了解直角三角形的应用,要求学生借助坡角关系构造直角三角形,并结合图形利用三角函数解直角三角形,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{a+4}$ |
 如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=$\sqrt{3}$,则AB的长是( )
如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=$\sqrt{3}$,则AB的长是( )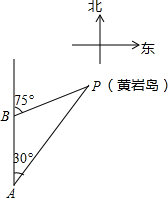 如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1)
如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1)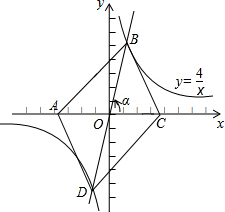 如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕原点O逆时针旋转α度(0<α<90)后的图形,若它与反比例函数y=$\frac{4}{x}$的图象分别交一、三象限的点B、D,已知点A(-m,0)、C(m,0)(m>0)
如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕原点O逆时针旋转α度(0<α<90)后的图形,若它与反比例函数y=$\frac{4}{x}$的图象分别交一、三象限的点B、D,已知点A(-m,0)、C(m,0)(m>0)