题目内容
1. 如图,两个圆的圆心为O,大圆半径OC,OD交小圆于点A,B,判断AB与CD的位置关系,并说明原因.
如图,两个圆的圆心为O,大圆半径OC,OD交小圆于点A,B,判断AB与CD的位置关系,并说明原因.
分析 利用半径相等得到OA=OB,OC=OD,则根据等腰三角形的性质得∠OAB=∠OBA,∠OCD=∠ODC,于是根据三角形内角和可得∠OAB=$\frac{1}{2}$(180°-∠O),∠OCD=$\frac{1}{2}$(180°-∠O),则∠OAB=∠OCD,然后根据平行线的判定方法可判断AB∥CD.
解答 解:AB∥CD.
∵OA=OB,OC=OD,
∴∠OAB=∠OBA,∠OCD=∠ODC,
∴∠OAB=$\frac{1}{2}$(180°-∠O),∠OCD=$\frac{1}{2}$(180°-∠O),
∴∠OAB=∠OCD,
∴AB∥CD.
点评 本题考查了圆的认识:圆可以看做是所有到定点O的距离等于定长r的点的集合,掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了平行线的判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.若-5x2ym与xny是同类项,则mn的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.下列图形中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
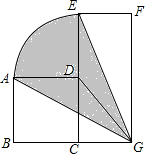 已知正方形ABCD的边长为a,长方形CEFG的边CE长为2a,边CG长为b.求以D为圆心,AD为半径的弧与GA,GE所围成的阴影部分的面积(用含a,b的代数式表示).
已知正方形ABCD的边长为a,长方形CEFG的边CE长为2a,边CG长为b.求以D为圆心,AD为半径的弧与GA,GE所围成的阴影部分的面积(用含a,b的代数式表示).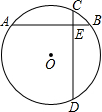 如图,在⊙O中,弦AB⊥CD于E,已知AE=5,CE=1,BE=3.求⊙O的半径.
如图,在⊙O中,弦AB⊥CD于E,已知AE=5,CE=1,BE=3.求⊙O的半径. 如图所示,已知正方形的边长是a.
如图所示,已知正方形的边长是a.