题目内容
如图，BD是∠ABC的平分线，DE∥BC交AB于点E，若∠BDE=25°，则∠ABD的度数为（ ）| A、50° | B、25° |
| C、15° | D、12.5° |
考点：平行线的性质
专题：
分析：根据平行线的性质以及角平分线的性质即可得出∠ABD的度数等于∠BDE，然后将∠BDE=25°代入即可得出答案．
解答：解：∵BD是∠ABC的平分线，
∴∠ABD=∠DBC，
∵DE∥BC，
∴∠DBC=∠BDE，
∴∠ABD=∠BDE，
∵∠BDE=25°，
∴∠ABD=25°．
故选：B．
∴∠ABD=∠DBC，
∵DE∥BC，
∴∠DBC=∠BDE，
∴∠ABD=∠BDE，
∵∠BDE=25°，
∴∠ABD=25°．
故选：B．
点评：本题主要考查了平行线的性质，角平分线的性质，解题的关键是：根据平行线的性质，角平分线的性质得到∠ABD=∠BDE．
练习册系列答案
相关题目
如图，P是定长线段AB上一点，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB先向左运动（C在线段AP上，D在线段BP上）．
如图，A、B、C、D在同一条直线上，∠EAD=∠FAD，∠EDA=∠FDA，则图中共有全等三角形（ ）| A、3对 | B、4对 | C、5对 | D、6对 |
不等式组
的解集在数轴上表示正确的是（ ）
|
A、 |
B、 |
C、 |
D、 |
世界杯比赛中，根据场上攻守形势，守门员会在门前来回跑动，如果以球门线为基准，向前跑记作正数，返回则记作负数，一段时间内，某守门员的跑动情况记录如下（单位：m）：+10，-2，+5，-6，+12，-9，+4，-14．（假定开始计时时，守门员正好在球门线上）
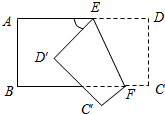如图，把一张长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠AED′=50°，则∠EFB等于（ ）| A、50° | B、55° |
| C、60° | D、65° |
如图，已知△ABC三个顶点的坐标分别为（1，2），（-2，3），（-1，0），把它们的横坐标和纵坐标都扩大到原来的2倍，得到点A′，B′，C′．下列说法正确的是（ ）| A、△A′B′C′与△ABC是位似图形，位似中心是点（1，0） |
| B、△A′B′C′与△ABC是位似图形，位似中心是点（-1，0） |
| C、△A′B′C′与△ABC是位似图形，位似中心是点（0，0） |
| D、△A′B′C′与△ABC是相似图形，但不是位似图形 |