题目内容
 如图所示,矩形ABCD中,AB=2,BC=3,P为BC边上与BC两点不重合的任意一点.设PA=x,D到PA的距离为y,则y与x的函数关系式为
如图所示,矩形ABCD中,AB=2,BC=3,P为BC边上与BC两点不重合的任意一点.设PA=x,D到PA的距离为y,则y与x的函数关系式为考点:矩形的性质,根据实际问题列反比例函数关系式
专题:
分析:把已知的线段用含x、y的代数式表示出来,转化到两个三角形中,易证其相似,从而得出关系式,进而求出x的取值范围.
解答:解:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAE=∠APB,
∵DE⊥AP,∴∠AED=90°,
∴∠B=∠AED=90°,
∴△ABP∽△DEA;
∴
=
,
即:
=
,
∴y=
,
故答案为:y=
,
∵AP为直角三角形ABP的斜边,AB=2,
∴AP>2,即x>2,
∵当点P移动到点C时AP最长,
∴AP=x=
=
=
,
∵AP<
,
∴2<x<
,
故答案为:2<x<
.
∴AD∥BC,∠B=90°,
∴∠DAE=∠APB,

∵DE⊥AP,∴∠AED=90°,
∴∠B=∠AED=90°,
∴△ABP∽△DEA;
∴
| AB |
| DE |
| AP |
| DA |
即:
| 2 |
| y |
| x |
| 3 |
∴y=
| 6 |
| x |
故答案为:y=
| 6 |
| x |
∵AP为直角三角形ABP的斜边,AB=2,
∴AP>2,即x>2,
∵当点P移动到点C时AP最长,
∴AP=x=
| AB2+BC2 |
| 22+32 |
| 13 |
∵AP<
| 13 |
∴2<x<
| 13 |
故答案为:2<x<
| 13 |
点评:此题主要利用了相似三角形的性质,利用性质建立已知和未知之间的联系是关键,根据图形化到相应的部分中,运用相关知识解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知|a|=5,
=3,且ab<0,则a-b=( )
| b2 |
| A、8 | B、-2 |
| C、8或-8 | D、2或-2 |
 如图,D为△ABC的BC边的中点,E为AC边上的一点,AC=3CE,BE和AD交于G点,则AG:GD=( )
如图,D为△ABC的BC边的中点,E为AC边上的一点,AC=3CE,BE和AD交于G点,则AG:GD=( )| A、2 | B、3 | C、3或4 | D、4 |
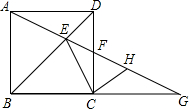 如图所示,在正方形ABCD中,点F在CD边上,射线AF交BD于点E,交BC的延长线于点G.求证:
如图所示,在正方形ABCD中,点F在CD边上,射线AF交BD于点E,交BC的延长线于点G.求证: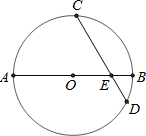 如图,AB是⊙O的直径,弦CD与AB相交于点E,AE=13,BE=3,cos∠AEC=
如图,AB是⊙O的直径,弦CD与AB相交于点E,AE=13,BE=3,cos∠AEC=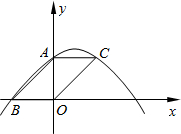 如图,?ABOC的顶点A、B、C在二次函数
如图,?ABOC的顶点A、B、C在二次函数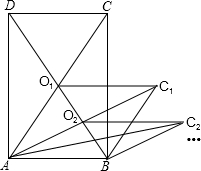 如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两边邻作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABC7O7的面积为
如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两边邻作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABC7O7的面积为