题目内容
12. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车:④当甲、乙两车相距50千米时,$t=\frac{5}{4}$或$\frac{15}{4}$.其中不正确的结论是③④(填序号)
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车:④当甲、乙两车相距50千米时,$t=\frac{5}{4}$或$\frac{15}{4}$.其中不正确的结论是③④(填序号)
分析 观察图象可判断①②,由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,可得出答案.
解答 解:由图象可知A、B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,
∴①②都正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得$\left\{\begin{array}{l}{m+n=0}\\{4m+n=300}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=100}\\{n=-100}\end{array}\right.$,
∴y乙=100t-100,
令y甲=y乙,可得:60t=100t-100,
解得:t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,
∴③不正确;
令|y甲-y乙|=50,可得|60t-100t+100|=50,即|100-40t|=50,
当100-40t=50时,可解得t=$\frac{5}{4}$,
当100-40t=-50时,可解得t=$\frac{15}{4}$,
又当t=$\frac{5}{6}$时,y甲=50,此时乙还没出发,
当t=$\frac{25}{6}$时,乙到达B城,y甲=250;
综上可知当t的值为$\frac{5}{4}$或$\frac{15}{4}$或$\frac{5}{6}$或t=$\frac{25}{6}$时,两车相距50千米,
∴④不正确;
综上可知不正确是:③④,
故答案为:③④.
点评 本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意t是甲车所用的时间.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案| A. | $\left\{\begin{array}{l}{20x+60y=280}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{60x+20y=280}\\{x-y=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{20x+60y=280}\\{y-x=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{60x+20y=280}\\{y-x=2}\end{array}\right.$ |
 如图,已知O是直线MN上的一点,∠AOB=90°,经过点O的直线DC平分∠BON,∠1=38°,求∠3和∠DOA的度数.
如图,已知O是直线MN上的一点,∠AOB=90°,经过点O的直线DC平分∠BON,∠1=38°,求∠3和∠DOA的度数.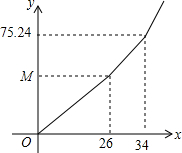 某市为鼓励居民节约用水,实行新的阶梯水价,即按用水量进行分段收费,阶段水价方案主要分为三档:
某市为鼓励居民节约用水,实行新的阶梯水价,即按用水量进行分段收费,阶段水价方案主要分为三档: 如图,AB=10cm,点C、D在AB上,且CB=4cm,D是AC的中点.
如图,AB=10cm,点C、D在AB上,且CB=4cm,D是AC的中点.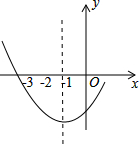 如图是二次函数y=ax2+bx-1图象的一部分,其对称轴为x=-1,且过点(-3,0),则(a+b+1)(2-a-b)=2.
如图是二次函数y=ax2+bx-1图象的一部分,其对称轴为x=-1,且过点(-3,0),则(a+b+1)(2-a-b)=2.