题目内容
10.如图1,△ABC为等腰三角形,AB=AC=6,P点是底边BC上的一个动点.PD∥AC,PE∥AB.(1)求四边形ADPE的周长;
(2)点P运动到什么位置时,四边形ADPE是菱形,请说明理由;
(3)如果ABC不是等腰三角形(图2)其他条件不变,点P运动到什么位置时,四边形ADPE是菱形,并说明理由.
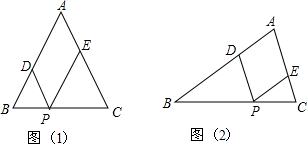
分析 (1)根据平行线的性质和等腰三角形的性质证明∠B=∠DPB,∠C=∠EPC,进而可得DB=DP,PE=EC,从而可得四边形ADPE的周长=AD+DP+PE+AE=AB+AC;
(2)当P运动到BC中点时,四边形ADPE是菱形;首先证明四边形ADPE是平行四边形,再证明DP=PE即可得到四边形ADPE是菱形;
(3)P运动到∠A的平分线上时,四边形ADPE是菱形,首先证明四边形ADPE是平行四边形,再根据平行线的性质可得∠1=∠3,从而可证出∠2=∠3,进而可得AE=EP,然后可得四边形ADPE是菱形.
解答 解:(1)∵PD∥AC,PE∥AB,
∴∠DPB=∠C,∠EPC=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠DPB,∠C=∠EPC,
∴DB=DP,PE=EC,
∴四边形ADPE的周长是:AD+DP+PE+AE=AB+AC=12;
(2)当P运动到BC中点时,四边形ADPE是菱形;
∵PD∥AC,PE∥AB,
∴四边形ADPE是平行四边形,
∴PD=AE,PE=AD,
∵PD∥AC,PE∥AB,
∴∠DPB=∠C,∠EPC=∠B,
∵P是BC中点,
∴PB=PC,
在△DBP和△EPC中,
$\left\{\begin{array}{l}{∠B=∠EPC}\\{BP=CP}\\{∠C=∠DPB}\end{array}\right.$,
∴△DBP≌△EPC(ASA),
∴DP=EC,
∵EC=PE,
∴DP=EP,
∴四边形ADPE是菱形;
(3)P运动到∠A的平分线上时,四边形ADPE是菱形,
∵PD∥AC,PE∥AB,
∴四边形ADPE是平行四边形,
∵AP平分∠BAC,
∴∠1=∠2,
∵AB∥EP,
∴∠1=∠3,
∴∠2=∠3,
∴AE=EP,
∴四边形ADPE是菱形.
点评 此题主要考查了菱形的判定,等腰三角形的性质,关键是掌握一组邻边相等的平行四边形是菱形.

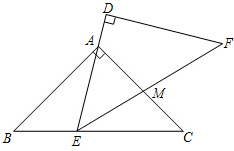 如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=$\sqrt{2}$.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:(1)BC=2;
如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=$\sqrt{2}$.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:(1)BC=2; 在△ABC中,AE为角平分线,AD为中线,CF⊥AE,AB=8,AC=6,求DF的长.
在△ABC中,AE为角平分线,AD为中线,CF⊥AE,AB=8,AC=6,求DF的长.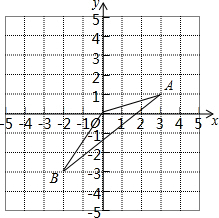 如图,已知A(3,1),B(-2,-3).
如图,已知A(3,1),B(-2,-3).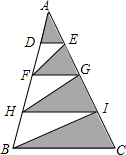 如图,三角形ABC中,将AB,AC分别四等分,已知三角形ADE的面积是6cm2,求阴影部分的面积.
如图,三角形ABC中,将AB,AC分别四等分,已知三角形ADE的面积是6cm2,求阴影部分的面积.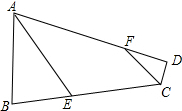 如图,在四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,分别交BC,AD于点E,F.
如图,在四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,分别交BC,AD于点E,F.