题目内容
1.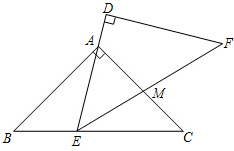 如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=$\sqrt{2}$.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:(1)BC=2;
如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=$\sqrt{2}$.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:(1)BC=2;(2)在△DEF运动过程中,△AEM能否构成等腰三角形?若能,请求出BE的长;若不能,请说明理由.
分析 (1)利用等腰直角三角形的性质和勾股定理可得结果;
(2)利用分类讨论的思想:①若AE=AM 则∠AME=∠AEM=45°,∠AME=∠C=45°,由外角性质可得此种情况不存在;②若AE=EM,则得△ABE≌△ECM,由全等三角形的性质,易得CE=AB=$\sqrt{2}$,BC=2,易得BE;③若MA=ME,则∠MAE=∠AEM=45°,证得AE平分∠BAC,利用等腰三角形的“三线合一”,可得BE=$\frac{1}{2}BC$=1.
解答 解:(1)∵△ABC是等腰直角三角形,∠BAC=90°,AB=AC=$\sqrt{2}$,
∴BC=$\sqrt{{AB}^{2}{+AC}^{2}}$=2,
故答案为:2;
(2)①若AE=AM 则∠AME=∠AEM=45°,
∵∠C=45°,
∴∠AME=∠C,
又∵∠AME>∠C,
∴这种情况不成立;
②若AE=EM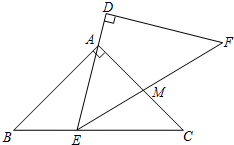 ,
,
∵∠B=∠AEM=45°,
∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°,
∴∠BAE=∠MEC,
在△ABE和△ECM中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠BAE=∠CEM}\\{AE=EM}\end{array}\right.$,
∴△ABE≌△ECM(AAS),
∴CE=AB=$\sqrt{2}$,
∵BC=2,
∴BE=2-$\sqrt{2}$;
③若MA=ME 则∠MAE=∠AEM=45°,
∵∠BAC=90°,
∴∠BAE=45°,
∴AE平分∠BAC,
∵AB=AC,
∴BE=$\frac{1}{2}BC$=1.
点评 本题主要考查了等腰直角三角形的性质和等腰三角形的性质,利用勾股定理,分类讨论是解答此题的关键.

练习册系列答案
相关题目
11.计算(3x3)2的结果是( )
| A. | 6x3 | B. | 9x6 | C. | 8x6 | D. | 8x5 |
 如图,M是?ABCD的AB边的中点,CM与BD相交于点E,连接DM,设?ABCD的面积为1,求图中阴影部分的面积.
如图,M是?ABCD的AB边的中点,CM与BD相交于点E,连接DM,设?ABCD的面积为1,求图中阴影部分的面积. 如图,
如图,