题目内容
15.解分式方程:$\frac{x}{x-2}-\frac{8}{{{x^2}-4}}=1$.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:方程两边乘以(x+2)(x-2),得x(x+2)-8=(x+2)(x-2),
解这个方程,得x=2,
经检验x=2是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
5.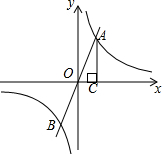 如图,已知点A(x,y)为反比例函数y=$\frac{k}{x}$(k>0)图象位于第一象限上一点,射线AO交双曲线y=$\frac{k}{x}$的另一支于点B,过点A作AC⊥x轴,连接BC.当点A的横坐标x逐渐增大时,则△ABC的面积( )
如图,已知点A(x,y)为反比例函数y=$\frac{k}{x}$(k>0)图象位于第一象限上一点,射线AO交双曲线y=$\frac{k}{x}$的另一支于点B,过点A作AC⊥x轴,连接BC.当点A的横坐标x逐渐增大时,则△ABC的面积( )
 如图,已知点A(x,y)为反比例函数y=$\frac{k}{x}$(k>0)图象位于第一象限上一点,射线AO交双曲线y=$\frac{k}{x}$的另一支于点B,过点A作AC⊥x轴,连接BC.当点A的横坐标x逐渐增大时,则△ABC的面积( )
如图,已知点A(x,y)为反比例函数y=$\frac{k}{x}$(k>0)图象位于第一象限上一点,射线AO交双曲线y=$\frac{k}{x}$的另一支于点B,过点A作AC⊥x轴,连接BC.当点A的横坐标x逐渐增大时,则△ABC的面积( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 不变 | D. | 不确定 |
3.若x2+2mx+36是完全平方式,则m=( )
| A. | 6 | B. | ±6 | C. | 12 | D. | ±12 |
7.已知一个多项式减去-2m结果等于m2+3m+2,这个多项式是( )
| A. | m2+5m+2 | B. | m2-m-2 | C. | m2-5m-2 | D. | m2+m+2 |
4.下列各式中,去括号正确的是( )
| A. | -(-2x+3)=2x-3 | B. | -(2x-3)=2x+3 | C. | -(-2x-3)=-2x+3 | D. | -(2x+3)=-2x+3 |
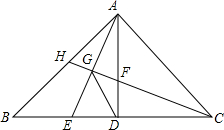 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.