题目内容
4．
如图，点C在线段AE上，BC∥DE，AC=DE，BC=CE．求证：AB=CD．
分析 利用SAS证明△ABC≌△DCE，根据全等三角形的对应边相等即可得到AB=CD．
解答 解：∵BC∥DE
∴∠ACB=∠E，
在△ABC和△DCE中
∵$\left\{\begin{array}{l}AC=DE\\∠ACB=∠E\\ BC=CD\end{array}\right.$
∴△ABC≌△DCE（SAS）
∴AB=CD．
点评 本题考查了全等三角形的性质定理与判定定理，解决本题的关键是证明△ABC≌△DCE（SAS）．
练习册系列答案
阅读快车系列答案
相关题目
14．
如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，BE=4，则AD的长是（ ）
如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，BE=4，则AD的长是（ ）| A． | 4 | B． | 2 | C． | 6 | D． | 2$\sqrt{3}$ |
15．
如图，在正方形ABCD中，△BCE是等边三角形，连接BD交CE于点M，若AB=$\sqrt{3}$，则EM的长为（ ）
如图，在正方形ABCD中，△BCE是等边三角形，连接BD交CE于点M，若AB=$\sqrt{3}$，则EM的长为（ ）| A． | 3-$\sqrt{3}$ | B． | 2$\sqrt{3}$-3 | C． | 2-$\sqrt{3}$ | D． | $\sqrt{3}$-1 |
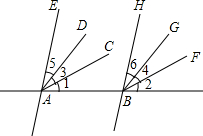如图，下列说法：
如图，已知△ABC与△ADE为等边三角形，D为BC延长线上的一点．
如图，在?ABCD中，对角线AC、BD相交成的锐角为α，若AC=a，BD=b，试用含b，c，α的式子表示?ABCD的面积．
如图，甲、乙两人同时从A地出发，分别以3km/h和4km/h的速度步行，甲向正南方向，乙向正东方向，1.5h后两人相距多远？