题目内容
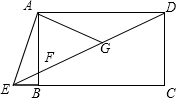 如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点.
如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点.(1)若BE=2,AG=4,求AB的长;
(2)若BC=2AB,求∠AED的度数.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:
分析:(1)根据矩形的性质得出∠BAD=∠ABC=∠ABE=90°,AD∥BC,求出∠ADE=∠CED,根据直角三角形性质求出∠AEG=∠AGE,推出AE=AG=4,根据勾股定理求出即可;
(2)过G作GH⊥AB于H,求出GH=AB,AE=AG=GF,证Rt△GHF≌Rt△ABE,推出∠AFG=∠AEB,求出∠EFB=∠AEB=3∠CED,得出4∠CED=90°,即可求出答案.
(2)过G作GH⊥AB于H,求出GH=AB,AE=AG=GF,证Rt△GHF≌Rt△ABE,推出∠AFG=∠AEB,求出∠EFB=∠AEB=3∠CED,得出4∠CED=90°,即可求出答案.
解答:解:(1)∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠ABE=90°,AD∥BC,
∴∠ADE=∠CED,
∵G为DF的中点,
∴AG=DG=EG,
∴∠ADE=∠GAD,
∴∠AGE=∠GAD+∠ADG=2∠ADG,
∵∠AED=2∠CED,
∴∠AEG=∠AGE,
∴AE=AG=4,
在Rt△ABE中,BE=2,AE=4,由勾股定理得:AB=
=2
;
(2)
过G作GH⊥AB于H,
∵∠DAB=90°,
∴GH∥AD,
∵G为DF中点,
∴AH=HF,
∴GH=
AD=
BC,
∵BC=2AB,
∴AB=GH,
∵∠BAD=90°,G为DF中点,
∴AG=GF,
∵AG=AE,
∴AE=GF,
在Rt△GHF和Rt△ABE中
∴Rt△GHF≌Rt△ABE(HL),
∴∠AFG=∠AEB,
∵∠AED=2∠CED,∠AFG=∠EFB,
∴∠EFB=∠AEB=3∠CED,
∵∠ABE=90°,
∴4∠CED=90°,
∴∠CED=22.5°,
∴∠AED=2∠CED=45°.
∴∠BAD=∠ABC=∠ABE=90°,AD∥BC,
∴∠ADE=∠CED,
∵G为DF的中点,
∴AG=DG=EG,
∴∠ADE=∠GAD,
∴∠AGE=∠GAD+∠ADG=2∠ADG,
∵∠AED=2∠CED,
∴∠AEG=∠AGE,
∴AE=AG=4,
在Rt△ABE中,BE=2,AE=4,由勾股定理得:AB=
| 42-22 |
| 3 |
(2)

过G作GH⊥AB于H,
∵∠DAB=90°,
∴GH∥AD,
∵G为DF中点,
∴AH=HF,
∴GH=
| 1 |
| 2 |
| 1 |
| 2 |
∵BC=2AB,
∴AB=GH,
∵∠BAD=90°,G为DF中点,
∴AG=GF,
∵AG=AE,
∴AE=GF,
在Rt△GHF和Rt△ABE中
|
∴Rt△GHF≌Rt△ABE(HL),
∴∠AFG=∠AEB,
∵∠AED=2∠CED,∠AFG=∠EFB,
∴∠EFB=∠AEB=3∠CED,
∵∠ABE=90°,
∴4∠CED=90°,
∴∠CED=22.5°,
∴∠AED=2∠CED=45°.
点评:本题考查了矩形的性质,全等三角形的性质和判定,三角形的内角和定理,直角三角形斜边上中线性质的应用,能综合运用性质进行推理是解此题的关键,题目综合性比较强,有一定的难度,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
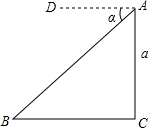 如图,飞机在空中A处探测得地面目标B处的俯角为α,此时飞机高度为AC=a,则BC的长度是( )
如图,飞机在空中A处探测得地面目标B处的俯角为α,此时飞机高度为AC=a,则BC的长度是( )| A、a•tanα | ||
B、
| ||
C、
| ||
D、
|
 如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.
如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.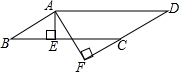 如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.
如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长. 如图,要把边长为6的正三角形剪成一个最大的正六边形,
如图,要把边长为6的正三角形剪成一个最大的正六边形,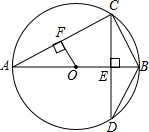 如图,AB为⊙O的直径,CD⊥AB,垂足为点E,交⊙O于点C和点D,OF⊥AC,垂足为点F.
如图,AB为⊙O的直径,CD⊥AB,垂足为点E,交⊙O于点C和点D,OF⊥AC,垂足为点F. 如图,如果∠1=40°,∠2=40°,∠3=40°,可判定哪些直线平行,请说明所用的判定方法.
如图,如果∠1=40°,∠2=40°,∠3=40°,可判定哪些直线平行,请说明所用的判定方法.