题目内容
 如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.
如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.考点:圆周角定理,锐角三角函数的定义
专题:
分析:先根据圆周角定理得出∠ADC=∠B,∠ACB=90°,再根据勾股定理求出AC的长,进而可得出结论.
解答:解:∵AB是⊙O的直径,
∴∠ACB=90°.
∵BC=3,AB=5,
∴AC=
=4.
∵∠ADC与∠B是同弧所对的圆周角,
∴tan∠ADC=tan∠B=
=
.
∴∠ACB=90°.
∵BC=3,AB=5,
∴AC=
| 52-32 |
∵∠ADC与∠B是同弧所对的圆周角,
∴tan∠ADC=tan∠B=
| AC |
| BC |
| 4 |
| 3 |
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
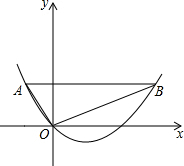 如图,在平面直的坐标角坐标系中,已知点A为(-1,
如图,在平面直的坐标角坐标系中,已知点A为(-1,
 为了适应车流量的增加,想把桥洞改为双行道,并且要使宽为1.2米,高为2.8米的卡车能安全通过,那么此桥洞的宽至少应增加多少米?
为了适应车流量的增加,想把桥洞改为双行道,并且要使宽为1.2米,高为2.8米的卡车能安全通过,那么此桥洞的宽至少应增加多少米?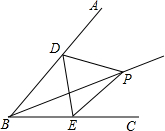 如图,已知点P是∠ABC的平分线与∠DEC的平分线的交点,求证:点P在∠ADE的平分线上.
如图,已知点P是∠ABC的平分线与∠DEC的平分线的交点,求证:点P在∠ADE的平分线上.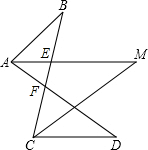 (1)如图所示,已知∠B=32°,∠D=38°,AM,CM分别平分∠BAD和∠BCD,求∠M的度数.
(1)如图所示,已知∠B=32°,∠D=38°,AM,CM分别平分∠BAD和∠BCD,求∠M的度数. 如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,AB=2
如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,AB=2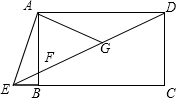 如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点.
如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点.