题目内容
 老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.
老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.(1)求证:∠BQM=60°;
(2)做完(1)后,同学们在老师的启发下进行了反思和探究,得出如下许多结论:
①若将题中的“BM=CN”与∠BQM=60°位置交换,则命题正确;
②若将题中的点M、N分别移动到BC、CA的延长线上,直线AM、BN交点为Q,则∠BQM=60°;
③若将题中的条件“点M、N分别在正△ABC的边BC、CA上”改为“点M、N分别在正方形ABCD的边BC、CD上”,且BM=CN,AM交BN于点Q,则∠BQM=90°;
④把③中的“BM=CN”与∠BQM=90°的位置互换,则命题正确;
…
请你判断上述四个结论正确的有
选择其中的一个结论给出你的证明(自己画出图形,然后结合图形证明)
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:如图,证明AB=BC,∠ABM=∠BCN;进而证明△ABM≌△BCN,得到∠QBM=∠BAM;结合∠BAM+∠QBM=90°,即可解决问题.
解答: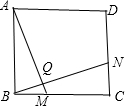 解:①②③④四个结论均正确;下面近就③给出证明如下:
解:①②③④四个结论均正确;下面近就③给出证明如下:
如图,∵四边形ABCD为正方形,
∴AB=BC,∠ABM=∠BCN;
在△ABM与△BCN中,
,
∴△ABM≌△BCN(SAS),
∴∠QBM=∠BAM;而∠BAM+∠QBM=90°,
∴∠QBM+∠BMQ=90°,
∴∠BQM=90°.
 解:①②③④四个结论均正确;下面近就③给出证明如下:
解:①②③④四个结论均正确;下面近就③给出证明如下:如图,∵四边形ABCD为正方形,
∴AB=BC,∠ABM=∠BCN;
在△ABM与△BCN中,
|
∴△ABM≌△BCN(SAS),
∴∠QBM=∠BAM;而∠BAM+∠QBM=90°,
∴∠QBM+∠BMQ=90°,
∴∠BQM=90°.
点评:该题主要考查了等边三角形、正方形的性质、全等三角形的判定及其性质的应等几何知识点问题;解题的关键是深入观察图形结构特点,数形结合,找出图形中隐含的等量关系或全等关系.

练习册系列答案
相关题目
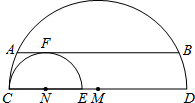 如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设
如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设
 如图,在△ABC中,D为AB边上一点,∠B=∠ACD,若AD=4,BD=3,求AC的长.
如图,在△ABC中,D为AB边上一点,∠B=∠ACD,若AD=4,BD=3,求AC的长.
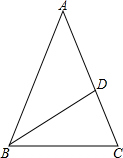 如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于D.
如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于D.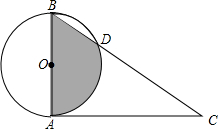 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,∠C=30°.
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,∠C=30°.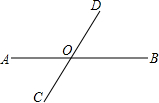 如图,直线AB,CD相交于点O,∠AOD比∠BOD大60°,求∠AOD与∠BOD的大小.
如图,直线AB,CD相交于点O,∠AOD比∠BOD大60°,求∠AOD与∠BOD的大小. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F.