题目内容
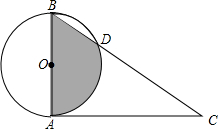 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,∠C=30°.
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,∠C=30°.(1)求BD的长;
(2)求阴影部分的面积.
考点:切线的性质,扇形面积的计算
专题:计算题
分析:(1)根据切线的性质得BA⊥CA,则∠BAC=90°,则利用互余可计算出∠B=60°,易得△OBD为等边三角形,所以BD=OB=1;
(2)由△OBD为等边三角形得到∠BOD=60°,则∠AOD=120°,然后根据等边三角形的面积公式和扇形的面积公式,利用阴影部分的面积=S△OBD+S扇形OAD进行计算即可.
(2)由△OBD为等边三角形得到∠BOD=60°,则∠AOD=120°,然后根据等边三角形的面积公式和扇形的面积公式,利用阴影部分的面积=S△OBD+S扇形OAD进行计算即可.
解答:解: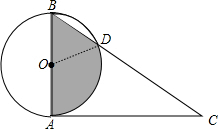 (1)∵CA切⊙O于A,
(1)∵CA切⊙O于A,
∴BA⊥CA,
∴∠BAC=90°,
∵∠C=30°,
∴∠B=60°,
∵OB=OD,
∴△OBD为等边三角形,
∴BD=OB=1;
(2)∵△OBD为等边三角形,
∴∠BOD=60°,
∴∠AOD=120°,
∴阴影部分的面积=S△OBD+S扇形OAD
=
×12+
=
+
.
 (1)∵CA切⊙O于A,
(1)∵CA切⊙O于A,∴BA⊥CA,
∴∠BAC=90°,
∵∠C=30°,
∴∠B=60°,
∵OB=OD,
∴△OBD为等边三角形,
∴BD=OB=1;
(2)∵△OBD为等边三角形,
∴∠BOD=60°,
∴∠AOD=120°,
∴阴影部分的面积=S△OBD+S扇形OAD
=
| ||
| 4 |
| 120•π•12 |
| 360 |
=
| ||
| 4 |
| π |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了等边三角形的判定与性质和扇形的面积公式.

练习册系列答案
相关题目
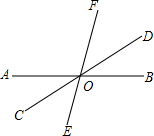 如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数.
如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数. 如图,请你数出五角星中同旁内角的对数.
如图,请你数出五角星中同旁内角的对数. 老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.
老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.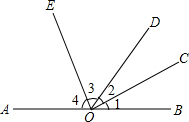 如图,O为直线AB上一点,OC平分∠BOD,EO⊥OC,垂足为点O,试判断∠3与∠4的关系.
如图,O为直线AB上一点,OC平分∠BOD,EO⊥OC,垂足为点O,试判断∠3与∠4的关系.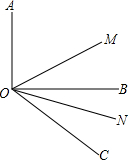 如图,OA⊥OB,OC为射线,OM平分∠AOC,ON平分∠BOC.
如图,OA⊥OB,OC为射线,OM平分∠AOC,ON平分∠BOC.