题目内容
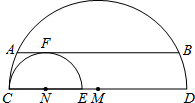 如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设
如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设 |
| CD |
 |
| CE |
考点:切线的性质,勾股定理,垂径定理
专题:计算题
分析:过M作MG⊥AB于G,连MB,NF,如图,设⊙M,⊙N的半径分别为R,r,根据垂径定理得BG=AG=
AB=2,在Rt△MBG中,利用勾股定理可计算出MB2-MG2=BG2=4,即R2-MG2=4,接着根据切线的性质得NF⊥AB,易判断四边形MGFN为矩形,得到MG=NF=r,则R2-r2=4,利用圆的周长公式得到z(x+y)=(CD-CE)(π•R+π•r),然后变形得到(R2-r2)•2π,再利用整体代入的方法计算.
| 1 |
| 2 |
解答:解:过M作MG⊥AB于G,连MB,NF,如图,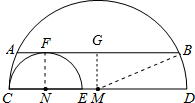 设⊙M,⊙N的半径分别为R,r,
设⊙M,⊙N的半径分别为R,r,
∵MG⊥AB,
∴BG=AG=
AB=2,
在Rt△MBG中,MB2-MG2=BG2=22=4,
即R2-MG2=4,
又∵大半圆M的弦与小半圆N相切于点F,
∴NF⊥AB,
∵AB∥CD,
∴四边形MGFN为矩形,
∴MG=NF=r,
∴z(x+y)=(CD-CE)(π•R+π•r)
=(2R-2r)(R+r)•π
=(R2-r2)•2π
=4•2π
=8π.
故答案为8π.
 设⊙M,⊙N的半径分别为R,r,
设⊙M,⊙N的半径分别为R,r,∵MG⊥AB,
∴BG=AG=
| 1 |
| 2 |
在Rt△MBG中,MB2-MG2=BG2=22=4,
即R2-MG2=4,
又∵大半圆M的弦与小半圆N相切于点F,
∴NF⊥AB,
∵AB∥CD,
∴四边形MGFN为矩形,
∴MG=NF=r,
∴z(x+y)=(CD-CE)(π•R+π•r)
=(2R-2r)(R+r)•π
=(R2-r2)•2π
=4•2π
=8π.
故答案为8π.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了勾股定理和垂径定理.

练习册系列答案
相关题目
 如图,已知正△ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG=x,设△EFG的面积为y,则y关于x的函数关系式为( )
如图,已知正△ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG=x,设△EFG的面积为y,则y关于x的函数关系式为( )A、-
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、
|
 如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.
如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.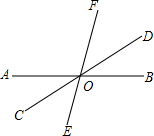 如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数.
如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数. 如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=1,DC=2,点P是AB上的动点,则PC+PD的最小值为
如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=1,DC=2,点P是AB上的动点,则PC+PD的最小值为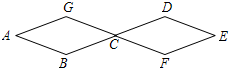 如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEF的顺序按菱形的边循环运动,行走2015厘米后停下,则这只蚂蚁停在( )
如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEF的顺序按菱形的边循环运动,行走2015厘米后停下,则这只蚂蚁停在( ) 老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.
老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.