题目内容
9. 如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为$\sqrt{7}$-1.
如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为$\sqrt{7}$-1.
分析 过点M作MF⊥DC于点F,根据在边长为2的菱形ABCD中,∠A=60°,M为AD中点,得到2MD=AD=CD=2,从而得到∠FDM=60°,∠FMD=30°,进而利用锐角三角函数关系求出EC的长即可.
解答  解:如图所示:过点M作MF⊥DC于点F,
解:如图所示:过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FD=$\frac{1}{2}$MD=$\frac{1}{2}$,
∴FM=DM×cos30°=$\frac{\sqrt{3}}{2}$,
∴MC=$\sqrt{F{M}^{2}+C{F}^{2}}$=$\sqrt{7}$,
∴EC=MC-ME=$\sqrt{7}$-1.
故答案为:$\sqrt{7}$-1.
点评 此题主要考查了菱形的性质以及锐角三角函数关系等知识,解题的关键是从题目中抽象出直角三角形,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.九年级一班和二班每班选8名同学进行投篮比赛,每名同学投篮10次,对每名同学投中的次数进行统计,甲说:“一班同学投中次数为6个的最多”乙说:“二班同学投中次数最多与最少的相差6个.”上面两名同学的议论能反映出的统计量是( )
| A. | 平均数和众数 | B. | 众数和极差 | C. | 众数和方差 | D. | 中位数和极差 |
14.在-1,-2,0,1这4个数中最小的一个是( )
| A. | -1 | B. | 0 | C. | -2 | D. | 1 |
1.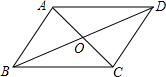 如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
 如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )| A. | AB=AD | B. | AC⊥BD | C. | AC=BD | D. | ∠BAC=∠DAC |
19.方程2x+3=7的解是( )
| A. | x=5 | B. | x=4 | C. | x=3.5 | D. | x=2 |
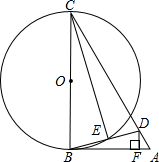 如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.
如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.