题目内容
5. 如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )
如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )| A. | 2 | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
分析 先根据勾股定理的逆定理判断出△ABC的形状,再由锐角三角函数的定义即可得出结论.
解答 解:∵由图可知,AC2=22+42=20,BC2=12+22=5,AB2=32+42=25,
∴△ABC是直角三角形,且∠ACB=90°,
∴cos∠ABC=$\frac{BC}{AB}$=$\frac{\sqrt{5}}{5}$.
故选D.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
15.关于x的一元二次方程:x2-4x-m2=0有两个实数根x1、x2,则m2($\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$)=( )
| A. | $\frac{{m}^{4}}{4}$ | B. | $-\frac{{m}^{4}}{4}$ | C. | 4 | D. | -4 |
13.下列语句正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 有两边及一角对应相等的两个三角形全等 | |
| C. | 矩形的对角线相等 | |
| D. | 平行四边形是轴对称图形 |
17.九年级一班和二班每班选8名同学进行投篮比赛,每名同学投篮10次,对每名同学投中的次数进行统计,甲说:“一班同学投中次数为6个的最多”乙说:“二班同学投中次数最多与最少的相差6个.”上面两名同学的议论能反映出的统计量是( )
| A. | 平均数和众数 | B. | 众数和极差 | C. | 众数和方差 | D. | 中位数和极差 |
14.在-1,-2,0,1这4个数中最小的一个是( )
| A. | -1 | B. | 0 | C. | -2 | D. | 1 |
 如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)
如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)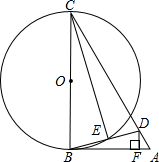 如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.
如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.