题目内容
14. 如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )
如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
分析 延长ED交BC于F,由平角的定义得到∠2=40°,根据三角形的外角的性质得到∠3=70°,根据平行线的性质即可得到结论.
解答  解:延长ED交BC于F,
解:延长ED交BC于F,
∵∠CDE=140°,
∴∠2=40°,
∵∠C=30°,
∴∠3=70°,
∵AB∥DE,
∴∠3=∠ABC=70°,
故选D.
点评 本题考查了三角形外角性质,平行线的性质的应用,解此题的关键掌握两直线平行,同位角相等.

练习册系列答案
相关题目
2.若a、b是关于x的一元二次方程x2-6x+n+1=0的两根,且等腰三角形三边长分别为a、b、4,则n的值为( )
| A. | 8 | B. | 7 | C. | 8或7 | D. | 9或8 |
9.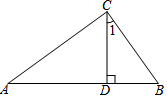 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠1的值为( )
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠1的值为( )
 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠1的值为( )
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠1的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
19. 如图,AB∥CD,AD=CD,∠1=70°30',则∠2的度数是( )
如图,AB∥CD,AD=CD,∠1=70°30',则∠2的度数是( )
 如图,AB∥CD,AD=CD,∠1=70°30',则∠2的度数是( )
如图,AB∥CD,AD=CD,∠1=70°30',则∠2的度数是( )| A. | 40°30' | B. | 39°30' | C. | 40° | D. | 39° |
3.将一张面值为50元的人民币,兑换成10元或20元的零钱,兑换方案有( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
4.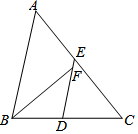 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )
 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )| A. | $\frac{5}{8}$ | B. | 1 | C. | $\frac{5}{2}$ | D. | 1.5 |
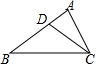 如图,点D是△ABC的AB边上一点,且AB=6,BD=4,AC=2$\sqrt{3}$.
如图,点D是△ABC的AB边上一点,且AB=6,BD=4,AC=2$\sqrt{3}$.