题目内容
 如图,△ABC中,∠C=90°,∠A=30°,已知AC=3,求周长.
如图,△ABC中,∠C=90°,∠A=30°,已知AC=3,求周长.考点:勾股定理,含30度角的直角三角形
专题:
分析:根据含30度角的直角三角形性质求出AB=2BC,设BC=x,根据勾股定理得出方程,求出方程的解即可.
解答:解:∵在△ABC中,∠C=90°,∠A=30°,AC=3,
∴AV=2BC,
设BC=x,则AB=2x,
由勾股定理得:32+x2=(2x)2,
解得:x=
,
即BC=
,AB=2
,
所以△ABC的周长为AC+BC+AB=3+
+2
=3+3
.
∴AV=2BC,
设BC=x,则AB=2x,
由勾股定理得:32+x2=(2x)2,
解得:x=
| 3 |
即BC=
| 3 |
| 3 |
所以△ABC的周长为AC+BC+AB=3+
| 3 |
| 3 |
| 3 |
点评:本题考查了勾股定理,含30度角的直角三角形性质的应用,解此题的关键是得出关于x的方程,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,几何体的俯视图是( )
如图所示,几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
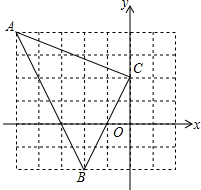 已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长.
已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长. 已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AB=10,BC=6.求:sin∠ACD的值及AD的长.
已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AB=10,BC=6.求:sin∠ACD的值及AD的长.
 直线在AB、CD相交于点O,OE平分∠BOD,若∠AOD:∠DOE=7:1,求∠AOC的度数.
直线在AB、CD相交于点O,OE平分∠BOD,若∠AOD:∠DOE=7:1,求∠AOC的度数. 如图所示的图形是一个物体的三视图,请画出这个物体的大致形状.
如图所示的图形是一个物体的三视图,请画出这个物体的大致形状. 画出y=x+0.5的函数图象.
画出y=x+0.5的函数图象.