题目内容
7.阅读下面的材料:∵ax2+bx+c=0(a≠0)的根为:x1=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,x2=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$
∴x1+x2=$\frac{-2b}{2a}=-\frac{b}{a}$,x1x2=$\frac{{b}^{2}-({b}^{2}-4ac)}{4{a}^{2}}$=$\frac{c}{a}$
综上得,设ax2+bx+c=0(a≠0)的根为x1、x2,则有x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$
请你根据这个结论解答下面问题:
(1)x2+bx+c=0的两根为3和-5,则b=-2,c=-15.
(2)已知x1、x2是方程x2+5x-2016=0的两个实数根,则(x1-1)(x2-1)=-2010.
分析 (1)由方程的两根分别为3和-5,结合x1+x2=-$\frac{b}{a}$、x1x2=$\frac{c}{a}$,即可求出b、c的值;
(2)根据根与系数的关系可得出x1+x2=-5、x1x2=-2016,将其代入(x1-1)(x2-1)=x1x2-(x1+x2)+1中,即可求出结论.
解答 解:(1)∵方程x2+bx+c=0的两根为3和-5,
∴-b=3-5=-2,c=3×(-5)=-15.
故答案为:-2;-15.
(2)∵x1、x2是方程x2+5x-2016=0的两个实数根,
∴x1+x2=-5,x1x2=-2016,
∴(x1-1)(x2-1)=x1x2-(x1+x2)+1=-2016-(-5)+1=-2010.
故答案为:-2010.
点评 本题考查了根与系数的关系,牢记x1+x2=-$\frac{b}{a}$、x1x2=$\frac{c}{a}$是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
18.下列调查方式,你认为最合适的是( )
| A. | 了解北京市每天的流动人口数,采用抽样调查方式 | |
| B. | 旅客上飞机前的安检,采用抽样调查方式 | |
| C. | 了解北京市居民”一带一路”期间的出行方式,采用全面调查方式 | |
| D. | 日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式 |
 中国传统数学最重要的著作《九章算术》中记载:“今有牛五、羊二,直金十两:牛二、羊五,直金八两.问牛、羊各直金几何?”其译文是:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两,问每头牛、每只羊各值金多少两?”现设每头牛值金x两,每只羊值金y两,则可列方程组为$\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$.
中国传统数学最重要的著作《九章算术》中记载:“今有牛五、羊二,直金十两:牛二、羊五,直金八两.问牛、羊各直金几何?”其译文是:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两,问每头牛、每只羊各值金多少两?”现设每头牛值金x两,每只羊值金y两,则可列方程组为$\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$.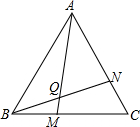 学完“轴对称”这一章后,老师布置了一道思考题:如图所示,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求证:∠BQM=60°
学完“轴对称”这一章后,老师布置了一道思考题:如图所示,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求证:∠BQM=60°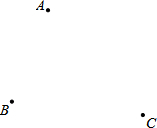 如图,平面上有三个点A,B,C,利用尺规按要求作图;
如图,平面上有三个点A,B,C,利用尺规按要求作图;