题目内容
15.某超市进行装修,若请A、B两个装修队同时施工,6天可以完成,需付两队装修费共3600元,若先请A队单独做4天,再请B队单独做9天可以完成,需付装修费3500元.(1)A、B两装修队工作一天,超市各应付多少元给他们?
(2)已知A队单独完成需10天,B队单独完成需求15天,单独请哪个队超市所需费用最少?
(3)若装修完,超市每天可赢利200元,你认为如何安排施工更有利于超市?请说明理由.
分析 (1)设A每天费用为x元,B每天费用为y元,根据题意可得等量关系:①A、B两个装修队同时施工,6天可以完成,需付两队费用共3600元;②甲队单独做4天,再请乙队单独做9天可以完成,需付两队费用共3500元,根据费用列出方程组,解方程组即可;
(2)分别求出AB两队的施工费用,再进行比较即可;
(3)分别求出A单独做,B单独做和A,B合作需要的费用,再作出比较.
解答 解:(1)设:A队工作一天商店应付x元,B队工作一天超市付y元.
由题意得$\left\{\begin{array}{l}{6x+6y=3600}\\{4x+9y=3500}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=380}\\{y=220}\end{array}\right.$,
答:A、B两装修队工作一天,超市各应付380元和220元给他们;
(2)单独请A队需要的费用:380×10=3800元.
单独请B队需要的费用:15×220=3300元.
答:单独请B队需要的费用少;
(3)请两队同时装修,理由:
A单独做,需费用3800元,少赢利200×10=2000元,相当于损失5800元;
B单独做,需费用3300元,少赢利200×15=3000元,相当于损失6300元;
A、B合作,需费用3600元,少赢利200×6=1200元,相当于损失4800元;
因为4800<5800<6300,
所以A、B合作损失费用最少.
答:A、B合作施工更有利于商店.
点评 此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
3.水是人类宝贵的资源.为鼓励居民节约用水,某市自来水公司对全市用户采用分段计费的方式计算水费,收费标准知下图所示.
若某用户要使5月的水费平均不超过每吨2.5元,则该用户5月最多用水为多少吨?
| 月用水量 | 不超过12t的部分 | 超过12t且不超过18t的部分 | 超过18t的部分 |
| 每吨收费标准(元) | 2 | 2.5 | 3 |
 两个同样的直角三角板如图所示摆放,使点F,B,E,C在一条直线上,则有DF∥AC,理由是内错角相等两直线平行
两个同样的直角三角板如图所示摆放,使点F,B,E,C在一条直线上,则有DF∥AC,理由是内错角相等两直线平行 如图,小方格都是边长为1的正方形,分别以格点A,B为圆心,1为半径作半圆,再以格点C为圆心,2为半径作$\frac{1}{4}$圆,则阴影部分的面积为π-2.
如图,小方格都是边长为1的正方形,分别以格点A,B为圆心,1为半径作半圆,再以格点C为圆心,2为半径作$\frac{1}{4}$圆,则阴影部分的面积为π-2.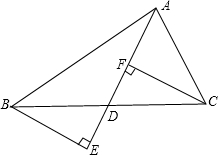 如图,已知AD为△ABC的中线,延长AD,分别过点B,C作BE⊥AD,CF⊥AD.
如图,已知AD为△ABC的中线,延长AD,分别过点B,C作BE⊥AD,CF⊥AD.