题目内容
14. 如图,在矩形ABCD中,点E是CD上一点,AB=AE,BF⊥AE,垂足为F.求证:BF=BC.
如图,在矩形ABCD中,点E是CD上一点,AB=AE,BF⊥AE,垂足为F.求证:BF=BC.
分析 连接BE,作EM⊥AB于M,先证明四边形BCEM是矩形,再证明△ABF≌△AEM,即可解决问题.
解答 证明:连接BE,作EM⊥AB于M,
∵四边形ABCD是平行四边形,
∴∠ABC=∠C=90°,
∵∠EMB=∠MBC=∠C=90°,
∴四边形BCEM是矩形,
∴EM=BC,
在△ABF和△AEM中,
$\left\{\begin{array}{l}{∠BAF=∠MAE}\\{∠AME=∠AFB=90°}\\{AB=AE}\end{array}\right.$,
∴△ABF≌△AEM,
∴BF=ME=BC.
点评 本题考查全等三角形的判定和性质、矩形的性质,添加辅助线构造全等三角形是解决问题的关键,学会常用辅助线添加方法,属于中考常考题型.

练习册系列答案
相关题目
5.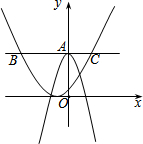 如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )
如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )
 如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )
如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )| A. | 1 | B. | 4.5 | C. | 3 | D. | 6 |
2.已知反比例函数y=$\frac{k}{x}$的图象经过点(2,6),那么k的值为( )
| A. | 12 | B. | 3 | C. | -3 | D. | -12 |
19.国家提倡“低碳减排”,某公司计划在海边建风能发电站,电站年均发电量约为216000000度,若将数据216000000用科学记数法表示为( )
| A. | 216×106 | B. | 21.6×107 | C. | 2.16×108 | D. | 2.16×109 |
6.某校从各年级随机抽取50名学生,每人进行10次投篮,投篮进球次数如下表所示:该投篮进球数据的中位数是( )
| 次数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | 8 | 10 | 7 | 6 | 6 | 6 | 4 | 1 | 2 | 0 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 在三角形ABC中,∠C=90°,AC=5,BC=12,AB=13.则点B到AC的距离是12.
在三角形ABC中,∠C=90°,AC=5,BC=12,AB=13.则点B到AC的距离是12.