题目内容
19．
已知，如图，AE是一条直线，O是AE上一点，OB，OD分别是∠AOC，∠EOC的平分线，猜想：OB与OD有什么位置关系？并说明理由．
分析 根据图示确立各角度数之间的关系，然后求出∠BOD的度数，再得出位置关系即可．
解答 解：OB与OD垂直，
∵O是直线AE上的一点，OB是∠AOC的平分线，OD是∠COE平分线，
∴∠AOE=180°，∠DOC=$\frac{1}{2}$∠COE，∠BOC=$\frac{1}{2}$∠AOC，
∴∠BOD=∠BOC+∠COD=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠COE=$\frac{1}{2}$（∠AOC+∠COE）=$\frac{1}{2}$∠AOE=90°，
∴OB与OD垂直．
点评 此题考查角的平分线，根据图示确立各角度数之间的关系，利用角平分线的性质来求．
练习册系列答案
相关题目
如图，已知线段a和b，a＞b，求作直角三角形ABC，使直角三角形的斜边AB=a，直角边AC=b．（用尺规作图，保留作图痕迹，不要求写作法）
10．某农场计划安排10个生产组来耕作30公顷土地，这些土地可以种蔬菜，也可以种水稻，种这些作物所需生产组及预计产值如表：
为了使所有土地都种上作物，且全部生产组都有工作，应安排多少个生产组种蔬菜？这时预计总产值为多少元？
| 每公顷所需生产组/个 | 每公顷雨季产值 | |
| 蔬菜 | $\frac{1}{2}$ | 52500 |
| 水稻 | $\frac{1}{4}$ | 18000 |
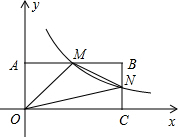如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，反比例函数y=$\frac{k}{x}$的图象经过点M，N，若M是AB的中点，△OMN的面积为3．
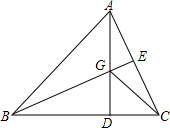如图，在△ABC中，点D，E分别在BC，AC边上，E为AC的中点，AD，BE交于点G，BD=2DC，S△GEC=2，S△GDC=4，则△ABC的面积是（ ）
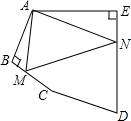如图，在五边形ABCDE中，∠BAE=120°，∠B=∠E=90°，AB=BC，AE=DE，在BC，DE上分别找出一点M，N，使得△AMN的周长最小时，则∠AMN+∠ANM的度数为多少？
8．体育文化用品店购进篮球和排球共40个，进价和售价如表，全部售完后共获利520元．
（1）购进篮球和排球各多少个？
（2）销售时，用6000元买了50个篮球和若干个排球，能获得利润多少？
| 篮球 | 排球 | |
| 进价（元/个） | 80 | 50 |
| 售价（元/个） | 95 | 60 |
（2）销售时，用6000元买了50个篮球和若干个排球，能获得利润多少？