题目内容
12.解不等式(组),并把解集表示在数轴上.(1)10-3(x+6)≤2(x-1)
(2)$\left\{\begin{array}{l}{\frac{2x-1}{3}-\frac{5x+1}{2}≤2}\\{5x-1<3(x+1)}\end{array}\right.$.
分析 (1)去括号,移项,合并同类项,系数化成1即可.
(2)根据不等式的性质求出不等式的解集,根据找不等式组解集的规律找出即可.
解答 解:(1)10-3(x+6)≤2(x-1),
10-3x-18≤2x-2,
-3x-2x≤18-10-2,
-5x≤6,
x≥-$\frac{6}{5}$,
把解集表示在数轴上为: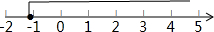 .
.
(2)$\left\{\begin{array}{l}{\frac{2x-1}{3}-\frac{5x+1}{2}≤2①}\\{5x-1<3(x+1)②}\end{array}\right.$
由①得:x≥-$\frac{17}{11}$,
由②得:x<2,
∴不等式解集是-$\frac{17}{11}$≤x<2.
不等式的解集在数轴上表示为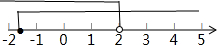 .
.
点评 本题主要考查对解一元一次不等式组,解一元一次不等式,不等式的性质,在数轴上表示不等式的解集等知识点的理解和掌握,能求出不等式组的解集并能在数轴上表示不等式组的解集是解此题的关键.

练习册系列答案
相关题目
4.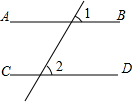 如图,由∠1=∠2得到AB∥CD的理由是( )
如图,由∠1=∠2得到AB∥CD的理由是( )
 如图,由∠1=∠2得到AB∥CD的理由是( )
如图,由∠1=∠2得到AB∥CD的理由是( )| A. | 两直线平行,同位角相等 | B. | 两直线平行,内错角相等 | ||
| C. | 同位角相等,两直线平行 | D. | 内错角相等,两直线平行 |
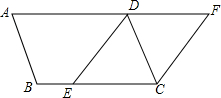 如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE.
如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE. 如图,△ABC的顶点坐标分别为(4,1),B(6,1),C(7,5)
如图,△ABC的顶点坐标分别为(4,1),B(6,1),C(7,5)