题目内容
12.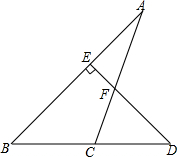 如图,DE⊥AB,∠A=25°,∠D=45°,求∠ACD的度数.
如图,DE⊥AB,∠A=25°,∠D=45°,求∠ACD的度数.
分析 先根据∠DEB=90°,求得∠B的度数,再根据三角形外角性质,求得∠ACD的度数.
解答 解:∵DE⊥AB,
∴∠DEB=90°,
∴∠B=90°-∠D=90°-45°=45°,
∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠B=25°+45°=70°.
点评 本题主要考查了三角形外角性质以及三角形内角和定理,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
3.下列运算正确的是( )
| A. | a3•a3=2a3 | B. | a0÷a3=a-3 | C. | (ab2)3=ab6 | D. | (a3)2=a5 |
20.小红去水果店买苹果,店内一欧四种苹果,各品种的单价如下表所示:
回家后,小红根据买的情况看列了一个方程50-12.4x-9(4-x)=3.8(设购买B品种的苹果x千克),像考考妈妈,下列说法与实际购买信息不符合的是( )
| 苹果品种 | A | B | C | D |
| 单价(元/千克) | 19 | 12.4 | 9 | 7 |
| A. | 一共买了4千克苹果 | B. | (4-x)表示买C品种苹果的千克数 | ||
| C. | 没有买A,D品种的苹果 | D. | 本次购买苹果共支出50元 |
7.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A瞬时针旋转到位置①可得到点P1,此时AP1=$\sqrt{2}$;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=$\sqrt{2}$+1;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=$\sqrt{2}$+2;…,按此规律继续旋转,直至得到点P2017为止,则AP2017长为( )


| A. | 1344+672$\sqrt{2}$ | B. | 1344+673$\sqrt{2}$ | C. | 1345+673$\sqrt{2}$ | D. | 1345+674$\sqrt{2}$ |
17. 如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )
如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )
 如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )
如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | 3-$\sqrt{5}$ | D. | $\sqrt{5}$-1 |
1.下列命题中真命题的个数( )
①无理数包括正无理数、零和负无理数;
②过一点有且只有一条直线与已知直线垂直;
③和为180°的两个角互为邻补角;
④正数有两个平方根,且这两个平方根之和等于0.
①无理数包括正无理数、零和负无理数;
②过一点有且只有一条直线与已知直线垂直;
③和为180°的两个角互为邻补角;
④正数有两个平方根,且这两个平方根之和等于0.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
2.小明拿来n个形状大小完全相同的正方体木块,整齐地摆放在桌上,其三视图如图所示,则n的值是( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
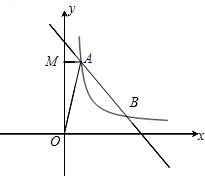 如图,一次函数y=mx+5的图象与反比例函数$y=\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
如图,一次函数y=mx+5的图象与反比例函数$y=\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,