题目内容
17. 如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )
如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | 3-$\sqrt{5}$ | D. | $\sqrt{5}$-1 |
分析 可设AD=x,由四边形EFDC与矩形ABCD相似,根据相似多边形对应边的比相等列出比例式,求解即可.
解答 解:∵AB=1,
设AD=x,则FD=x-1,FE=1,
∵四边形EFDC与矩形ABCD相似,
∴$\frac{EF}{FD}$=$\frac{AD}{AB}$,$\frac{1}{x-1}=\frac{x}{1}$,
解得x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$(不合题意舍去),
经检验x1=$\frac{1+\sqrt{5}}{2}$是原方程的解.
故选A.
点评 本题考查了翻折变换(折叠问题),相似多边形的性质,本题的关键是根据四边形EFDC与矩形ABCD相似得到比例式.

练习册系列答案
相关题目
8.在△ABC中,AB=AC,∠BAC=50°,则∠C的度数为( )
| A. | 75° | B. | 65° | C. | 55° | D. | 50° |
5.一次函数y=-2x+3的图象与x轴的交点坐标是( )
| A. | (0,3) | B. | (3,0) | C. | ($\frac{3}{2}$,0) | D. | ($\frac{2}{3}$,0) |
9.下列运算正确的是( )
| A. | 2a3•a4=2a7 | B. | a3+a4=a7 | C. | (2a4)3=8a7 | D. | a3÷a4=a |
7.下列图形:任取一个既是轴对称图形又是中心对称图形的概率是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
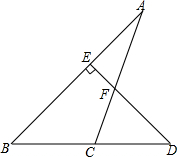 如图,DE⊥AB,∠A=25°,∠D=45°,求∠ACD的度数.
如图,DE⊥AB,∠A=25°,∠D=45°,求∠ACD的度数.