题目内容
11．计算（-$\sqrt{5}$）2+（$\sqrt{2}$）0-|$\sqrt{3}$-3|的结果是（ ）| A． | 3+$\sqrt{3}$ | B． | 9-$\sqrt{3}$ | C． | -$\sqrt{5}$-2 | D． | $\sqrt{5}$-2 |
分析 利用二次根式的性质、零指数幂的意义和绝对值的意义计算．
解答 解：原式=5+1+3-$\sqrt{3}$
=9-$\sqrt{3}$．
故选B．
点评 本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可．
练习册系列答案
相关题目
1．
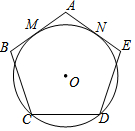如图，半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N，则劣弧MN的长度为（ ）
如图，半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N，则劣弧MN的长度为（ ）| A． | $\frac{1}{5}$π | B． | $\frac{2}{5}$π | C． | $\frac{\sqrt{3}}{5}$π | D． | $\frac{1}{3}$π |
2．市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如表（单位：环）：
（1）根据表格中的数据，分别计算甲、乙的平均成绩；
（2）已知甲六次成绩的方差S甲2=$\frac{2}{3}$，试计算乙六次测试成绩的方差；根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
（2）已知甲六次成绩的方差S甲2=$\frac{2}{3}$，试计算乙六次测试成绩的方差；根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．
用一段长30米的篱笆围成一个一边靠墙的矩形花圃，墙长为18米，另三边用篱笆恰好围成．围成的花圃是如图的矩形ABCD．设AB边的长为x米，花圃ABCD的面积为S平方米，则S与x之间的函数关系式是s=x（30-2x）．（不必写出自变量取值范围）
如图，已知AF∥EC，AB∥CD，∠A=65°，则∠C=65度．
20．$\frac{2•tan30°}{1-ta{n}^{2}30°}$的值等于（ ）
| A． | $\sqrt{3}$ | B． | -$\sqrt{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{-\sqrt{3}}{3}$ |
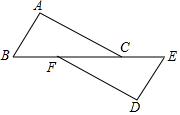已知：如图，点B、F、C、E在一条直线上，∠B=∠E，∠ACB=∠DFE，且BF=EC．求证：△ABC≌△DEF．