题目内容
1.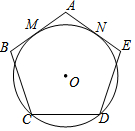 如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧MN的长度为( )
如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧MN的长度为( )| A. | $\frac{1}{5}$π | B. | $\frac{2}{5}$π | C. | $\frac{\sqrt{3}}{5}$π | D. | $\frac{1}{3}$π |
分析 连接OM,ON,首先根据切线的性质和正五边形的性质求得圆心角的度数,然后利用弧长公式进行计算.
解答 解:如图:连接OM,ON,
∵⊙O与正五边形ABCDE的边AB、AE相切于点M、N,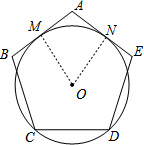
∴OM⊥AB,ON⊥AC,
∵∠A=108°,
∴∠MON=72°,
∵半径为1,
∴劣弧MN的长度为:$\frac{72π×1}{180}$=$\frac{2}{5}π$π,
故选B.
点评 本题考查了正多边形和圆的知识,解题的关键是能够连接OM和ON,从而求得劣弧所在扇形的圆心角,利用扇形弧长公式求解.

练习册系列答案
相关题目
16.某食品厂从生产的袋装食品中随机抽样检测20袋的质量是否符合标准质量,超过或不足的质量分别用正、负数表示,例如+3表示该袋食品超过标准质量3克,现记录如下:
(1)在抽取的样品中,任意挑选两袋,它们的质量相差最大多少克?
(2)食品包装袋中标有“净重500±2克”,这批样品中有几袋质量不合格?并请你计算出这20袋食品的合格率是多少?【产品的合格率=(一批产品中的合格产品数量÷这批产品总量)×100%】
(3)若标准质量为500克/袋,则这次抽样检测的总质量是多少克?
| 与标准质量的误差 (单位:克) | -4 | -2 | 0 | +1 | +2 | +3 |
| 袋数 | 5 | 3 | 3 | 4 | 2 | 3 |
(2)食品包装袋中标有“净重500±2克”,这批样品中有几袋质量不合格?并请你计算出这20袋食品的合格率是多少?【产品的合格率=(一批产品中的合格产品数量÷这批产品总量)×100%】
(3)若标准质量为500克/袋,则这次抽样检测的总质量是多少克?
11.计算(-$\sqrt{5}$)2+($\sqrt{2}$)0-|$\sqrt{3}$-3|的结果是( )
| A. | 3+$\sqrt{3}$ | B. | 9-$\sqrt{3}$ | C. | -$\sqrt{5}$-2 | D. | $\sqrt{5}$-2 |
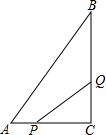 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动. 如图,半圆的半径为r,直角三角形的两条直角边分别为a,b,则图中阴影部分的面积是$\frac{1}{2}$πr2-$\frac{1}{2}$ab.
如图,半圆的半径为r,直角三角形的两条直角边分别为a,b,则图中阴影部分的面积是$\frac{1}{2}$πr2-$\frac{1}{2}$ab. 如图,将一个直径为1个单位长度的圆片上的点A放在原点,并把圆片沿数轴滚动1周,点A所在位置表示的数是±π.
如图,将一个直径为1个单位长度的圆片上的点A放在原点,并把圆片沿数轴滚动1周,点A所在位置表示的数是±π.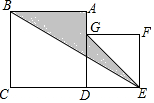 正方形ABCD与正方形DEFG如图所示摆放,正方形ABCD的边长为acm,正方形DEFG的边长为bcm.
正方形ABCD与正方形DEFG如图所示摆放,正方形ABCD的边长为acm,正方形DEFG的边长为bcm.