题目内容
14.某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的$\frac{1}{3}$后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.(1)按原计划完成总任务的$\frac{1}{3}$时,已抢修道路1200米;
(2)求原计划每小时抢修道路多少米?
分析 (1)按原计划完成总任务的$\frac{1}{3}$时,列式计算即可;
(2)设原计划每天修道路x米.根据原计划工作效率用的时间+实际工作效率用的时间=10等量关系列出方程.
解答 解:(1)按原计划完成总任务的$\frac{1}{3}$时,已抢修道路3600×$\frac{1}{3}$=1200米,
故答案为:1200米;
(2)设原计划每小时抢修道路x米,
根据题意得:$\frac{1200}{x}+\frac{3600-1200}{(1+50%)x}=10$,
解得:x=280,
经检验:x=280是原方程的解.
答:原计划每小时抢修道路280米.
点评 本题考查了分式方程的应用.分析题意,找到合适的等量关系是解决问题的关键.本题应用的等量关系为:工作时间=工作总量÷工效.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
4.若同一个圆的内接正三角形、正方形、正六边形的边长分别记作a3,a4,a6,则a3:a4:a6等于( )
| A. | 1:$\sqrt{2}$:$\sqrt{3}$ | B. | 1:2:3 | C. | 3:2:1 | D. | $\sqrt{3}$:$\sqrt{2}$:1 |
19.关于x的一元二次方程x2+x+m=0有实数根,则m的取值范围是( )
| A. | m≥$-\frac{1}{4}$ | B. | m≤$-\frac{1}{4}$ | C. | m≥$\frac{1}{4}$ | D. | m≤$\frac{1}{4}$ |
 由5个完全相同的正方体组成的立体图形如图所示,则它的俯视图是( )
由5个完全相同的正方体组成的立体图形如图所示,则它的俯视图是( )



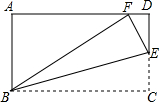 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为$\frac{5}{3}$.
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为$\frac{5}{3}$.