题目内容
19.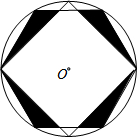 如图,在半径为2的⊙O中,两个顶点重合的内接正四边形与正六边形,则阴影部分的面积为6-2$\sqrt{3}$.
如图,在半径为2的⊙O中,两个顶点重合的内接正四边形与正六边形,则阴影部分的面积为6-2$\sqrt{3}$.
分析 如图,连接OB,OF,根据题意得:△BFO是等边三角形,△CDE是等腰直角三角形,求得△ABC的高和底即可求出阴影部分的面积.
解答 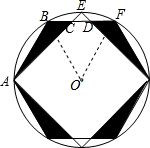 解:如图,连接OB,OF,
解:如图,连接OB,OF,
根据题意得:△BFO是等边三角形,△CDE是等腰直角三角形,
∴BF=OB=2,
∴△BFO的高为;$\sqrt{3}$,CD=2(2-$\sqrt{3}$)=4-2$\sqrt{3}$,
∴BC=$\frac{1}{2}$(2-4+2$\sqrt{3}$)=$\sqrt{3}$-1,
∴阴影部分的面积=4S△ABC=4×$\frac{1}{2}$($\sqrt{3}-1$)•$\sqrt{3}$=6-2$\sqrt{3}$.
故答案为:6-2$\sqrt{3}$.
点评 本题考查了正多边形和圆,三角形的面积,解题的关键是知道阴影部分的面积等于4个三角形的面积.

练习册系列答案
相关题目
10. 已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )
已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )
 已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )
已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )| A. | 4 | B. | 2 | C. | 1 | D. | $\sqrt{2}$ |
7.下列命题中,假命题是( )
| A. | 等边三角形是等腰三角形 | B. | 如果ab=0,那么a=0且b=0 | ||
| C. | 如果a>0,b<0,那么ab<0 | D. | 全等三角形的面积相等 |
4.若同一个圆的内接正三角形、正方形、正六边形的边长分别记作a3,a4,a6,则a3:a4:a6等于( )
| A. | 1:$\sqrt{2}$:$\sqrt{3}$ | B. | 1:2:3 | C. | 3:2:1 | D. | $\sqrt{3}$:$\sqrt{2}$:1 |
8.以下图形中对称轴的数量小于3的是( )
| A. |  | B. |  | C. |  | D. |  |
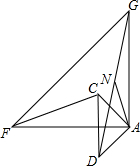 已知△ACD与△AGF都为等腰直角三角形,∠GAF=∠CAD=90°.连接GD、CF,N为线段GD的中点,连接AN.
已知△ACD与△AGF都为等腰直角三角形,∠GAF=∠CAD=90°.连接GD、CF,N为线段GD的中点,连接AN.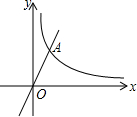 已知图中的曲线为反比例函数y=$\frac{k+2}{x}$(k为常数)的图象的一支.
已知图中的曲线为反比例函数y=$\frac{k+2}{x}$(k为常数)的图象的一支. 小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.
小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.