题目内容
19.下列说法正确的是( )| A. | $\sqrt{4-x}$有意义,则x≥4 | B. | 2x2-7在实数范围内不能因式分解 | ||
| C. | 方程x2+1=0无解 | D. | 方程x2=2x的解为 $x=±\sqrt{2x}$ |
分析 由二次根式有意义的条件,可得4-x≥0;由平方差公式可将2x2-7在实数范围内分解;由一元二次方程的解法,可求得答案.
解答 解:A、$\sqrt{4-x}$有意义,则4-x≥0,即x≤4;故本选项错误;
B、2x2-7=($\sqrt{2}$x+$\sqrt{7}$)($\sqrt{2}$x-$\sqrt{7}$),故本选项错误;
C、∵x2+1=0,
∴x2=-1,
∴方程x2+1=0无实数根,
故本选项正确;
D、∵x2=2x,
∴x2-2x=0,
∴x(x-2)=0,
解得:x1=0,x2=2,
故本选项错误.
故选C.
点评 此题考查了二次根式有意义的条件、实数范围内的因式分解以及一元二次方程的解法.注意掌握因式分解的方法与一元二次方程的解法.

练习册系列答案
相关题目
9.Rt△ABC中,∠C=90°,tanA=$\frac{3}{5}$,BC=5,则AB=( )
| A. | 3 | B. | 4 | C. | $\frac{25}{3}$ | D. | $\frac{5\sqrt{34}}{3}$ |
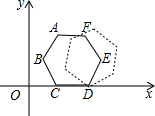 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.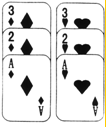 如图,是从一副扑克牌中取出的两组牌,分别是红桃1、2、3和方块1、2、3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张,求摸出的两张牌的牌面数字之和小于5的概率.(要求用列表或树状图表示)
如图,是从一副扑克牌中取出的两组牌,分别是红桃1、2、3和方块1、2、3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张,求摸出的两张牌的牌面数字之和小于5的概率.(要求用列表或树状图表示)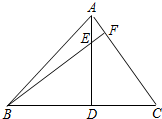 已知在△ABC中,AD⊥BC,垂足D点在边BC上,BF⊥AC分别交射线DA、射线CA于点E、F,若BD=4,∠BAD=45°.
已知在△ABC中,AD⊥BC,垂足D点在边BC上,BF⊥AC分别交射线DA、射线CA于点E、F,若BD=4,∠BAD=45°.