题目内容
5.从-2,-1,0,1,2,3,4这7个数中任选一个数作为a的值,则使得关于x的分式方程$\frac{3-ax}{x-3}+3=\frac{x}{3-x}$有整数解,且关于x的一次函数y=(a+1)x+a-4的图象不经过第二象限的概率是$\frac{2}{7}$.分析 首先使得关于x的分式方程$\frac{3-ax}{x-3}+3=\frac{x}{3-x}$有整数解,且关于x的一次函数y=(a+1)x+a-4的图象不经过第二象限的数,然后直接利用概率公式求解即可求得答案.
解答 解:∵关于x的分式方程$\frac{3-ax}{x-3}+3=\frac{x}{3-x}$有整数解,
∴3-ax+3(x-3)=-x,
解得:x=$\frac{6}{4-a}$,
∵x≠3,
∴a≠2,
∴当a=-2,1,3时,分式方程$\frac{3-ax}{x-3}+3=\frac{x}{3-x}$有整数解;
∵关于x的一次函数y=(a+1)x+a-4的图象不经过第二象限,
∴a+1>0,a-4≤0,
∴-1<a≤4,
∴当a=0,1,2,3,4时,关于x的一次函数y=(a+1)x+a-4的图象不经过第二象限;
综上,当a=1,3时,使得关于x的分式方程$\frac{3-ax}{x-3}+3=\frac{x}{3-x}$有整数解,且关于x的一次函数y=(a+1)x+a-4的图象不经过第二象限;
∴使得关于x的分式方程$\frac{3-ax}{x-3}+3=\frac{x}{3-x}$有整数解,且关于x的一次函数y=(a+1)x+a-4的图象不经过第二象限的概率是:$\frac{2}{7}$.
故答案为:$\frac{2}{7}$.
点评 此题考查了概率公式的应用、一次函数的图象与系数的关系以及分式方程的解.注意根据题意求得使得关于x的分式方程$\frac{3-ax}{x-3}+3=\frac{x}{3-x}$有整数解,且关于x的一次函数y=(a+1)x+a-4的图象不经过第二象限的数是关键.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | 四个数2、3、5、4的中位数为4 | |
| B. | 了解重庆初三学生备战中考复习情况,应采用普查 | |
| C. | 小明共投篮25次,进了10个球,则小明进球的概率是0.4 | |
| D. | 从初三体考成绩中抽取100名学生的体考成绩,这100名考生是总体的一个样本 |
14.数据4,2,6的平均数和方差分别是( )
| A. | 2,$\frac{8}{3}$ | B. | 2,$\frac{4}{3}$ | C. | 4,$\frac{8}{3}$ | D. | 4,$\frac{4}{3}$ |
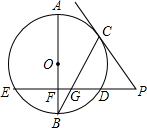 如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.
如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.
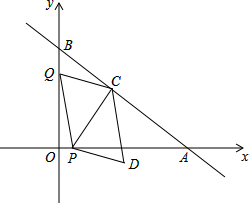 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(8,0),B(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造?PQCD,设点P运动的时间为t秒.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(8,0),B(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造?PQCD,设点P运动的时间为t秒. 已知命题“如果两条平行线被第三条直线所截,那么一对同位角的平分线互相平行”
已知命题“如果两条平行线被第三条直线所截,那么一对同位角的平分线互相平行”