题目内容
如图，在Rt△ABC中，∠ACB=90°，M，N分别为AC，BC的中点，AN=5，BM=6，求AB的长．考点：勾股定理
专题：计算题
分析：设CM=x，CN=y，在直角三角形CBM与直角三角形ACN中，利用勾股定理列出两个关系式，相加求出x2+y2的值，在直角三角形ABC中，利用勾股定理求出AB的长即可．
解答：
解：设CM=AM=x，CN=BN=y，则有AC=2x，BC=2y，
在Rt△CBM中，根据勾股定理得：x2+4y2=36①，
在Rt△ACN中，根据勾股定理得：4x2+y2=25②，
①+②得：5x2+5y2=61，即x2+y2=
，
∴AB2=4x2+4y2=
，
则AB=
．
在Rt△CBM中，根据勾股定理得：x2+4y2=36①，
在Rt△ACN中，根据勾股定理得：4x2+y2=25②，
①+②得：5x2+5y2=61，即x2+y2=
| 61 |
| 5 |
∴AB2=4x2+4y2=
| 244 |
| 5 |
则AB=
2
| ||
| 5 |
点评：此题考查了勾股定理，熟练掌握勾股定理是解本题的关键．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
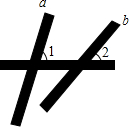（1）如图，三根木条相交成∠1、∠2，固定木条b、c，转动木条a，在木条a的转动过程中，∠1与∠2的大小关系发生了什么变化？木条a、b的位置关系发生了什么变化？
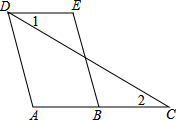已知：如图，AD∥BE，∠1=∠2，∠A=120°，求∠E的度数．正方形具有而菱形不一定具有的性质是（ ）
| A、四条边相等 |
| B、对角线互相垂直平分 |
| C、对角线平分一组对角 |
| D、对角线相等 |
如图，正方形ABCD的边长为4cm，则图中阴影部分的面积为（ ）| A、4 | B、8 | C、12 | D、16 |
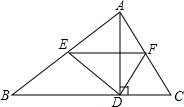如图，在△ABC中，AD是高．