题目内容
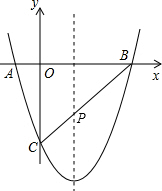
 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A和点B,AO:BO=1:5.CO=BO.△ABC的面积为15.
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A和点B,AO:BO=1:5.CO=BO.△ABC的面积为15.(1)求该二次函数的解析式;
(2)已知该函数图象的对称轴上存在一点P,使得△ACP的周长最小,请求出点P的坐标.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式,轴对称-最短路线问题
专题:
分析:(1)可设OA=x(x>0),则OB=OC=5x,根据三角形的面积可求得x的值,可求得A、B、C的坐标,利用待定系数法可求得抛物线的解析式;
(2)连接BC,交对称轴于点P,则P点即为所求,由B、C坐标可求得直线BC的解析式,可求得P点坐标.
(2)连接BC,交对称轴于点P,则P点即为所求,由B、C坐标可求得直线BC的解析式,可求得P点坐标.
解答:
解:
(1)设AO=x,则BO=CO=5x,
∴AB=6x,
∴S△ABC=
AB•OC=
×6x×5x=15x2,
又△ABC的面积为15,
解得x=1,
∴A(-1,0),B(5,0),C(0,-5),
设抛物线解析式为y=a(x+1)(x-5),
把C点坐标代入可得-5=-5a,解得a=1,
∴抛物线解析式为y=x2-4x-5;
(2)∵A、B关于对称轴对称,
∴连接BC交对称轴于一点,则该点即为所求的P点,如图,
设直线BC解析式为y=kx+b,
把B、C坐标代入可得
,解得
,
∴直线BC解析式为y=x-5,
由(1)可求得抛物线的对称轴为x=2,
在y=x-5中,令x=2可得y=-3,
∴P点坐标为(2,-3).
(1)设AO=x,则BO=CO=5x,
∴AB=6x,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
又△ABC的面积为15,
解得x=1,
∴A(-1,0),B(5,0),C(0,-5),
设抛物线解析式为y=a(x+1)(x-5),
把C点坐标代入可得-5=-5a,解得a=1,
∴抛物线解析式为y=x2-4x-5;
(2)∵A、B关于对称轴对称,
∴连接BC交对称轴于一点,则该点即为所求的P点,如图,

设直线BC解析式为y=kx+b,
把B、C坐标代入可得
|
|
∴直线BC解析式为y=x-5,
由(1)可求得抛物线的对称轴为x=2,
在y=x-5中,令x=2可得y=-3,
∴P点坐标为(2,-3).
点评:本题主要考查待定系数法及二次函数的对称性,在(1)中求得A、B、C的坐标是解题的关键,在(2)中确定出P点的位置是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
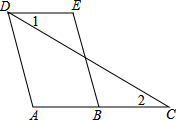 已知:如图,AD∥BE,∠1=∠2,∠A=120°,求∠E的度数.
已知:如图,AD∥BE,∠1=∠2,∠A=120°,求∠E的度数.
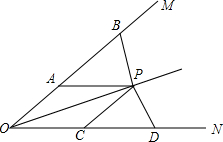 如图,OP平分∠MON,点A与B,点C与D分别在射线OM、ON上,且AB=CD
如图,OP平分∠MON,点A与B,点C与D分别在射线OM、ON上,且AB=CD


