题目内容
在△ABC中,∠ACB=α,∠BAC的外角平分线与∠ABC的外角平分线交于点D,过点D作DE⊥AB于点E,若BC=mBE.
(1)当α=90°,m=1时,探究DE和BE的数量关系.
(2)求
的值.

(1)当α=90°,m=1时,探究DE和BE的数量关系.
(2)求
| DE |
| BE |

考点:全等三角形的判定与性质,正方形的判定与性质,解直角三角形
专题:
分析:(1)过点D作DG⊥CG于点G,作DF⊥CA于点F,根据角平分线的性质可得出DF=DE=DG,故可得出四边形DFCG是正方形,再由全等三角形的判定定理得出△DGB≌△DEB,故可得出BE=BG,AE=AF,再根据m=1可知点B是CG的中点,由此可得出结论;
(2)过点D作DG⊥CG于点G,连接CD,根据角平分线的性质得出DE=DG=DF,由HL定理得出△DBE≌△DBG,故可得出BE=BG,DE=DG,再根据BC=mBE可知BC=mBG.根据HL定理得出△CDF≌△CDG,故CD是∠ACB的平分线,故∠DCG=
∠AB=
,再由锐角三角函数的定义即可得出结论.
(2)过点D作DG⊥CG于点G,连接CD,根据角平分线的性质得出DE=DG=DF,由HL定理得出△DBE≌△DBG,故可得出BE=BG,DE=DG,再根据BC=mBE可知BC=mBG.根据HL定理得出△CDF≌△CDG,故CD是∠ACB的平分线,故∠DCG=
| 1 |
| 2 |
| α |
| 2 |
解答:
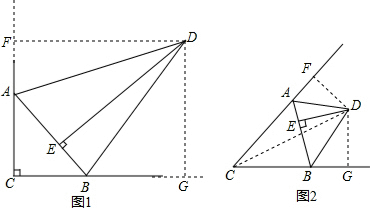 解:(1)如图1,过点D作DG⊥CG于点G,作DF⊥CA于点F,
解:(1)如图1,过点D作DG⊥CG于点G,作DF⊥CA于点F,
∵∠BAC的外角平分线与∠ABC的外角平分线交于点D,DE⊥AB,
∴DF=DE=DG,
∵∠C=90°,
∴四边形DFCG是正方形.
在△DGB与△DEB中,
,
∴△DGB≌△DEB(HL),
∴BE=BG,AE=AF,
∵m=1,
∴点B是CG的中点,
∴BG=
DG,即BE=
DE;
(2)如图2,过点D作DG⊥CG于点G,连接CD,
∵∠BAC的外角平分线与∠ABC的外角平分线交于点D,
∴DE=DG=DF,
在Rt△DBE与Rt△DBG中,
,
∴△DBE≌△DBG(HL),
∴BE=BG,DE=DG.
∵BC=mBE,
∴BC=mBG.
同理,△CDF≌△CDG,
∴CD是∠ACB的平分线,
∴∠DCG=
∠AB=
,
∴
=tan
,即
=tan
,
解得
=(m+1)•tan
.
 解:(1)如图1,过点D作DG⊥CG于点G,作DF⊥CA于点F,
解:(1)如图1,过点D作DG⊥CG于点G,作DF⊥CA于点F,∵∠BAC的外角平分线与∠ABC的外角平分线交于点D,DE⊥AB,
∴DF=DE=DG,
∵∠C=90°,
∴四边形DFCG是正方形.
在△DGB与△DEB中,
|
∴△DGB≌△DEB(HL),
∴BE=BG,AE=AF,
∵m=1,
∴点B是CG的中点,
∴BG=
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图2,过点D作DG⊥CG于点G,连接CD,
∵∠BAC的外角平分线与∠ABC的外角平分线交于点D,
∴DE=DG=DF,
在Rt△DBE与Rt△DBG中,
|
∴△DBE≌△DBG(HL),
∴BE=BG,DE=DG.
∵BC=mBE,
∴BC=mBG.
同理,△CDF≌△CDG,
∴CD是∠ACB的平分线,
∴∠DCG=
| 1 |
| 2 |
| α |
| 2 |
∴
| DG |
| BC |
| α |
| 2 |
| DE |
| (m+1)BE |
| α |
| 2 |
解得
| DE |
| BE |
| α |
| 2 |
点评:本题考查的是全等三角形的判定定理,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
下列说法中正确的是( )
| A、所有连接两点的线中,直线最短 |
| B、连接两点之间的线段叫做两点间的距离 |
| C、如果点P是线段AB的中点,那么AP=BP |
| D、如果AP=BP,那么点P是线段AB的中点 |
 如图,直线AB、CD相交于点O,若∠1+∠2=100°,则∠BOC等于( )
如图,直线AB、CD相交于点O,若∠1+∠2=100°,则∠BOC等于( )| A、130° | B、140° |
| C、150° | D、160° |
 AD是△ABC的高,下列能使△ABD≌ACD的条件是( )
AD是△ABC的高,下列能使△ABD≌ACD的条件是( )| A、BD=AC |
| B、∠B=45° |
| C、∠BAC=90° |
| D、AB=AC |
正方形具有而菱形不一定具有的性质是( )
| A、四条边相等 |
| B、对角线互相垂直平分 |
| C、对角线平分一组对角 |
| D、对角线相等 |
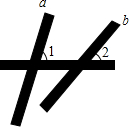 (1)如图,三根木条相交成∠1、∠2,固定木条b、c,转动木条a,在木条a的转动过程中,∠1与∠2的大小关系发生了什么变化?木条a、b的位置关系发生了什么变化?
(1)如图,三根木条相交成∠1、∠2,固定木条b、c,转动木条a,在木条a的转动过程中,∠1与∠2的大小关系发生了什么变化?木条a、b的位置关系发生了什么变化?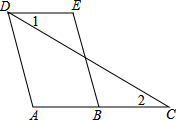 已知:如图,AD∥BE,∠1=∠2,∠A=120°,求∠E的度数.
已知:如图,AD∥BE,∠1=∠2,∠A=120°,求∠E的度数.