题目内容
7.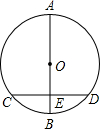 如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )| A. | 6 | B. | 8 | C. | 2$\sqrt{6}$ | D. | 4$\sqrt{5}$ |
分析 连接OC,根据题意求出OC、OE的长,根据勾股定理去CE,根据垂径定理得到答案.
解答 解: 连接OC,
连接OC,
∵AE=8,BE=2,
∴OC=5,OE=4,
由勾股定理得,CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=4,
∵AB为⊙0的直径,弦CD⊥AB,
∴CD=2CE=8,
故选:B.
点评 本题考查的是垂径定理和勾股定理的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.在同一平面直角坐标系内,将函数y=x-3的图象向右平移2个单位,再向下平移1个单位得到的图象与x轴的交点坐标是( )
| A. | (-6,0) | B. | (2,0) | C. | (6,0) | D. | (-1,0) |
15. 如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )
如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )
 如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )
如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )| A. | -2<b<0 | B. | -1<b<0 | C. | -$\frac{1}{2}$<b<0 | D. | 0<b<0 |
2.在平面直角坐标系中,点P(-2,5)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.沿海产业基地明湖广场占地面积约为14500m2,用科学记数法表示为( )
| A. | 1.45×106m2 | B. | 145×103m2 | C. | 1.45×104m2 | D. | 14.5×104m2 |
17.下列说法错误的是( )
| A. | 单项式x的系数和次数都是1 | |
| B. | $\frac{1}{2}$不是单项式 | |
| C. | 多项式3x2y+2xy-3x+y中一次项的系数分别是-3,1 | |
| D. | -$\frac{2xy}{3}$是系数为-$\frac{2}{3}$的二次单项式 |
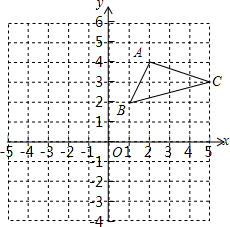 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4). 如图,已知点P在AB上,∠APD=∠APC,∠DBA=∠CBA,求证:AC=AD.
如图,已知点P在AB上,∠APD=∠APC,∠DBA=∠CBA,求证:AC=AD.