题目内容
11．在数轴上，点A所表示的实数为2，点B所表示的数为-1，⊙A的半径为4，则点B与⊙A的位置关系是点在圆内．分析 由已知条件得出AB=3，即d＜r，即可得出点B在⊙A的内部．
解答 解：∵点A所表示的实数为2，点B所表示的数为-1，
∴AB=2-（-1）=2+1=3＜⊙A的半径4，
即d＜r，
∴点B在⊙A的内部；
故答案为：点在圆内．
点评 本题考查了点与圆的位置关系；熟记d＜r，点在圆内；d=r，点在圆上；d＞r，点在园外是解决问题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
1．抛物线y=-x2+3x-2与坐标轴的交点共有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
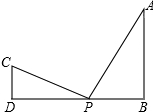如图，AB⊥DB于点B，CD⊥DB于点D，AB=6，CD=4，BD=14，点P在DB上移动．若以点C，D，P为顶点的三角形与点A，B，P为顶点的三角形相似，则DP=2或12或5.6．
如图，抛物线y1=-x2+2向右平移1个单位得到抛物线y2，则抛物线y2的顶点坐标为（1，2）；阴影部分的面积S=2．
在三角形纸片ABC中，∠C=90°，∠A=30°，AC=12，折叠该纸片，使点A和点B重合，折痕与AB、AC分别相交于点D和点E，（如图），折痕DE的长为4．
20．
如图，要使平行四边形ABCD成为菱形，需添加的一个条件是（ ）
如图，要使平行四边形ABCD成为菱形，需添加的一个条件是（ ）| A． | AB=BC | B． | AC=BD | C． | ∠ABC=90° | D． | AC与BD互相平分 |