题目内容
16.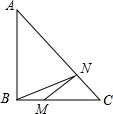 如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,点M在BC上,且BM=1,N是AC上一动点,则BN+MN的最小值为5.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,点M在BC上,且BM=1,N是AC上一动点,则BN+MN的最小值为5.
分析 过点B关于AC的对称点B′连接MB′,过点B′作B′E⊥BC,垂足为E.由等腰三角形三线合一的性质可知DB=$\frac{1}{2}AC$=2$\sqrt{2}$,从而得到BB′=4$\sqrt{2}$,由∠B′BC=45°可求得B′E=BE=4,故此可知ME=3,由勾股定理可知MB′=5.
解答 解:过点B关于AC的对称点B′连接MB′,过点B′作B′E⊥BC,垂足为E.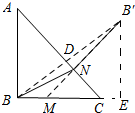
∵点B与B′关于AC对称,
∴BB′⊥AC,BD=DB′.
∵∠ABC=90°,AB=BC=4,
∴AC=$\sqrt{2}AB$=4$\sqrt{2}$.
∴BD=$\frac{1}{2}AC$=2$\sqrt{2}$.
∴BB′=4$\sqrt{2}$.
∵EB=B′E=4$\sqrt{2}×\frac{\sqrt{2}}{2}$=4,
∴ME=4-1=3.
在Rt△MB′E中,由勾股定理得:B′M=$\sqrt{M{E}^{2}+B′{E}^{2}}$=5.
故答案为:5.
点评 本题主要考查的是轴对称-路径最短、勾股定理、等腰直角三角形的性质,明确当B′、N、M在同一条直线上时,BN+MN有最小值是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
1.抛物线y=-x2+3x-2与坐标轴的交点共有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
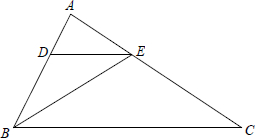 如图△ABC中,BE平分∠ABC,DE∥BC,若DE=2AD,AE=2,那么EC=4.
如图△ABC中,BE平分∠ABC,DE∥BC,若DE=2AD,AE=2,那么EC=4. 如图,已知∠BAC=∠DAC,请添加一个条件:AB=AD,使△ABC≌△ADC(写出一个即可).
如图,已知∠BAC=∠DAC,请添加一个条件:AB=AD,使△ABC≌△ADC(写出一个即可). 如图,△ABC中,∠B=40°,∠C=62°,AD⊥BC于点D,AE平分∠BAC,则∠DAE的度数是11°.
如图,△ABC中,∠B=40°,∠C=62°,AD⊥BC于点D,AE平分∠BAC,则∠DAE的度数是11°. 如图,△OAD≌△OBC,且∠O=60°,∠C=20°,则∠OAD=100°.
如图,△OAD≌△OBC,且∠O=60°,∠C=20°,则∠OAD=100°.