题目内容
5.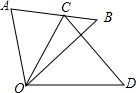 如图,△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形,点C恰好在边AB上.若∠AOD=100°,则∠D的度数是50°.
如图,△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形,点C恰好在边AB上.若∠AOD=100°,则∠D的度数是50°.
分析 已知△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,可得△COD≌△AOB,旋转角为40°,∵点C恰好在AB上,可得△AOC为等腰三角形,可结合三角形的内角和定理求∠B的度数.
解答 解:根据旋转性质得△COD≌△AOB,
∴CO=AO,∠D=∠B
由旋转角为40°,
∴∠AOC=∠BOD=40°,
∴∠OAC=(180°-∠AOC)÷2=70°,
∴∠BOC=∠AOD-∠AOC-∠BOD=20°,
∴∠AOB=∠AOC+∠BOC=60°,
在△AOB中,由内角和定理得∠B=180°-∠OAC-∠AOB=180°-70°-60°=50°.
∴∠D=∠B=50°
故答案为50°.
点评 此题是旋转的性质题,主要考查了旋转变化前后,对应角相等,同时充分用三角形的内角和定理,等腰三角形的性质,解本题的关键是用等腰三角形的性质求角的度数.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
15. 下列各展开图中,不能折成如图长方体的是( )
下列各展开图中,不能折成如图长方体的是( )
 下列各展开图中,不能折成如图长方体的是( )
下列各展开图中,不能折成如图长方体的是( )| A. |  | B. |  | C. |  | D. |  |
15.如图是某几何体的三视图,其侧面积( )


| A. | 2 | B. | 4 | C. | 2π | D. | π+2 |
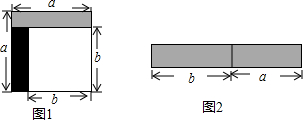 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).