题目内容
5．现有一枚均匀的正方体骰子，六个面分别标有数字1、2、3、4、5、6，连续抛掷两次，朝上的数字分别为a，b，已知直线l1：y=$\frac{1}{2}x-\frac{1}{2}$，直线l2：y=$\frac{a}{b}x+\frac{1}{b}$，（1）求直线l1∥l2的概率；
（2）求直线l1与l2的交点位于第一象限的概率．
分析 （1）首先根据题意列出表格，然后由表格即可求得所有等可能的结果与直线l1∥l2的情况，再利用概率公式即可求得答案；
（2）首先求得直线l1与l2的交点位于第一象限的情况，再利用概率公式即可求得答案．
解答 解：（1）列表法：
| 第一次 第二次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） |
| 5 | （1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） |
| 6 | （1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） |
∵直线l1∥l2，
∴$\frac{a}{b}$=$\frac{1}{2}$，
∴直线l1∥l2的有（1，2），（2，4），（3，6），
∴直线l1∥l2的概率为：$\frac{3}{36}$=$\frac{1}{12}$；
（2）解：∵直线l1与l2有交点，则b≠2a．
联立方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x-\frac{1}{2}}\\{y=\frac{a}{b}x+\frac{1}{b}}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=\frac{b+2}{b-2a}}\\{y=\frac{a+1}{b-2a}}\end{array}\right.$，
∵直线l1与l2的交点位于第一象限，则$\left\{\begin{array}{l}{x＞0}\\{y＞0}\end{array}\right.$，
即$\left\{\begin{array}{l}{\frac{b+2}{b-2a}＞0}\\{\frac{a+1}{b-2a}＞0}\end{array}\right.$，
解得b＞2a．
∴满足条件的实数对（a，b）有（1，3）、（1，4）、（1，5）、（1，6）、（2，5）、（2，6）共六种．
答：直线l1与l2的交点位于第一象限的概率为：$\frac{6}{36}$=$\frac{1}{6}$．
点评 此题考查了列表法或树状图法求概率以及一次函数的性质．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15．有一游泳池注满水，现按一定速度将水排尽，然后进行清洗，再按相同速度注满清水，使用一段时间后，又按相同的速度将水排尽，则游泳池的存水量为h（米）随时间t（小时）变化的大致图象是（ ）
| A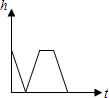． |  | B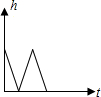． |  | C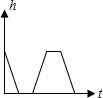． |  | D． |  |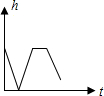
20．下列运算中，因式分解正确的是（ ）
| A． | -m2+mn-m=-m（m+n-1） | B． | 9abc-6a2b2=3bc（3-2ab） | ||
| C． | 3a2x-6bx+3x=3x（a2-2b） | D． | $\frac{1}{2}$ab2+$\frac{1}{2}$a2b=$\frac{1}{2}$ab（a+b） |
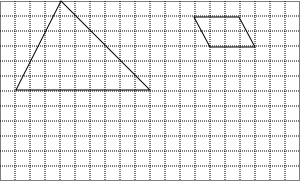如图，每个小正方形的边长都是1
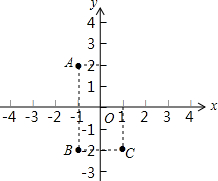如图所示：