题目内容
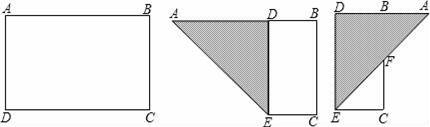
如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为( )

A.
 B.
B.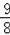
 C.2 D.4
C.2 D.4
C【考点】翻折变换(折叠问题).
【分析】根据折叠的性质,在图②中得到DB=8﹣6=2,∠EAD=45°;在图③中,得到AB=AD﹣DB=6﹣2=4,△ABF为等腰直角三角形,然后根据等腰三角形的性质和矩形的性质得到BF=AB=4,CF=BC﹣BF=6﹣4=2,EC=DB=2,最后根据三角形的面积公式计算即可.
【解答】解:∵AB=8,AD=6,纸片折叠,使得AD边落在AB边上,
∴DB=8﹣6=2,∠EAD=45°,
又∵△AED沿DE向右翻折,AE与BC的交点为F,
∴AB=AD﹣DB=6﹣2=4,△ABF为等腰直角三角形,
∴BF=AB=4,
∴CF=BC﹣BF=6﹣4=2,
而EC=DB=2,
 ×2×2=2.
×2×2=2.
故选:C.

【点评】本题考查了折叠的性质:折叠前后的两个图形全等,即对应线段相等,对应角相等.也考查了等腰三角形的性质和矩形的性质.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目

 的图象上的概率是 .
的图象上的概率是 .






 BD,EN=
BD,EN=