题目内容
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )


A.90° B.100° C.130° D.180°
B【考点】三角形内角和定理.
【分析】设围成的小三角形为△ABC,分别用∠1、∠2、∠3表示出△ABC的三个内角,再利用三角形的内角和等于180°列式整理即可得解.
【解答】解:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,
∠ABC=180°﹣60°﹣∠3=120°﹣∠3,
∠ACB=180°﹣60°﹣∠2=120°﹣∠2,
在△ABC中,∠BAC+∠ABC+∠ACB=180°,
∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,
∴∠1+∠2=150°﹣∠3,
∵∠3=50°,
∴∠1+∠2=150°﹣50°=100°.
故选:B.


【点评】本题考查了三角形的内角和定理,用∠1、∠2、∠3表示出△ABC的三个内角是解题的关键,也是本题的难点.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
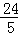 ,求GC的长.
,求GC的长.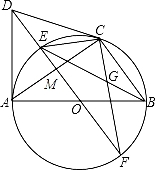
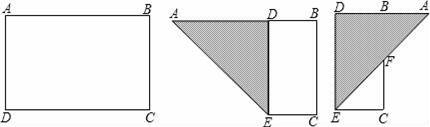


 B.
B.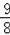


 ,则代数式x+y的值是_________
,则代数式x+y的值是_________