题目内容
10.若a>b,则下列式子正确的是( )| A. | -4a>-4b | B. | a-4>b-4 | C. | $\frac{1}{2}$a<$\frac{1}{2}$b | D. | 4-a>4-b |
分析 首先根据等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,可得a-4>b-4;然后根据不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变,可得$\frac{1}{2}$a>$\frac{1}{2}$b;最后根据不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变,可得-a<-b,-4a<-4b,所以4-a<4-b,据此判断即可.
解答 解:∵a>b,
∴a-4>b-4,
即选项B正确;
∵a>b,
∴$\frac{1}{2}$a>$\frac{1}{2}$b,
即选项C不正确;
∵a>b,
∴-a<-b,-4a<-4b,
∴4-a<4-b,
即选项A、D不正确;
故选:B.
点评 此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.

练习册系列答案
相关题目
18.若不等式组$\left\{\begin{array}{l}x<m\\ x>11\end{array}\right.$无解,则m的取值范围是( )
| A. | m<11 | B. | m>11 | C. | m≤11 | D. | m≥11 |
5.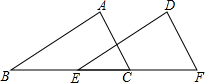 如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
 如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )| A. | BC=EF | B. | ∠ACB=∠F | C. | ∠B=∠DEF | D. | AB=DE |
2.下列计算结果正确的是( )
| A. | (x3)3=x6 | B. | a6•a4=a10 | C. | (ab4)4=ab8 | D. | (-3pq)2=-6p2q2 |
19.计算:(-a2)3( )
| A. | a6 | B. | -a6 | C. | a5 | D. | -a5 |
 如图小明在楼上点A处测得旗杆BC顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,旗杆的高度为16 m.
如图小明在楼上点A处测得旗杆BC顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,旗杆的高度为16 m. 解不等式组$\left\{\begin{array}{l}{2x-7<5-2x}\\{x+1>\frac{3+x}{2}}\end{array}\right.$,并将解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{2x-7<5-2x}\\{x+1>\frac{3+x}{2}}\end{array}\right.$,并将解集在数轴上表示出来.