题目内容
8.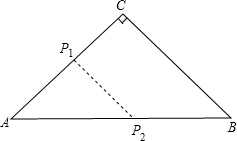 如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )
如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )| A. | S=t(100-t) | B. | S=$\frac{\sqrt{2}}{2}{t}^{2}-5\sqrt{2}t$ | C. | S=$\frac{\sqrt{2}}{2}{t}^{2}$ | D. | S=-$\frac{\sqrt{2}}{4}{t}^{2}+25\sqrt{2}t$ |
分析 首先求得AP1,AP2,进一步利用等腰直角三角形的性质求得△AP1P2,的高P1H,利用三角形的面积得出函数关系式即可.
解答 解:∵P1,P2分别从A,B出发,速度都是1cm/s,
∴t(s)后AP1=t,AP2=100-t,
作P1H⊥AP2,
∵△ABC为等腰直角三角形,
∴∠A=45°,
∴P1H=$\frac{\sqrt{2}}{2}$AP1=$\frac{\sqrt{2}}{2}$t,
∴S${\;}_{△A{P}_{1}{P}_{2}}$=$\frac{1}{2}$(100-t)×$\frac{\sqrt{2}}{2}$t=-$\frac{\sqrt{2}}{4}$t2+25$\sqrt{2}$t.
故选:D.
点评 此题考查动点问题,等腰直角三角形的性质,利用三角形的面积计算公式建立函数关系是解决问题的常用方法.

练习册系列答案
相关题目
3.有如图所示的几种几何体:

将它们按截面形状分成两类时,下面的分法不正确的是( )

将它们按截面形状分成两类时,下面的分法不正确的是( )
| A. | 截面可能是圆和三角形两类 | B. | 截面可能是圆和四边形两类 | ||
| C. | 截面可能是圆和五边形两类 | D. | 截面可能是三角形和四边形两类 |
 如图,利用关于坐标轴对称的点的坐标特点,画出△ABC关于x轴或y轴对称的图形.
如图,利用关于坐标轴对称的点的坐标特点,画出△ABC关于x轴或y轴对称的图形.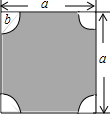 如图,四个角是半径为b的$\frac{1}{4}$的圆形.请用图中的字母表示阴影部分的面积.
如图,四个角是半径为b的$\frac{1}{4}$的圆形.请用图中的字母表示阴影部分的面积.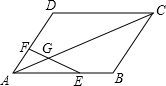 如图,在?ABCD中,E是AB的中点,点F在AD上,且$\frac{AF}{FD}$=$\frac{1}{2}$,EF交AC于点G,求$\frac{AG}{GC}$的值.
如图,在?ABCD中,E是AB的中点,点F在AD上,且$\frac{AF}{FD}$=$\frac{1}{2}$,EF交AC于点G,求$\frac{AG}{GC}$的值.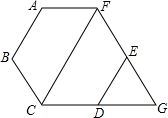 已知:如图,正六边形ABCDEF的边长为6cm.延长FE,CD相交于点G.
已知:如图,正六边形ABCDEF的边长为6cm.延长FE,CD相交于点G.
 如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.
如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.