题目内容
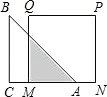
如图，已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米，AC与MN在同一直线上，开始时点A与点N重合，让△ABC以每秒2厘米的速度向左运动，最终点A与点M重合，则重叠部分面积y（厘米2）与时间t（秒）之间的函数关系式为__________．
y=
2．
【考点】根据实际问题列二次函数关系式．
【专题】压轴题；动点型．
【分析】根据△ABC是等腰直角三角形，则重叠部分也是等腰直角三角形，根据三角形的面积公式即可求解．
【解答】解：AM=20﹣2t，
则重叠部分面积y=
×AM2=2，
y=2（0≤t≤10）．
故答案为：y=2（0≤t≤10）
【点评】根据题意，找到所求量的等量关系是解决问题的关键．需注意AM的值的求法．
练习册系列答案
相关题目
，花园的一边靠墙，另三边用总长为40m的栅栏围
成（如
（m），花园的面积为
（m
）．
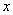之间的函数关系式，并写出自变量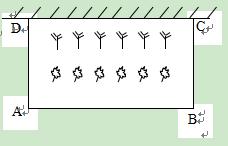
，当函数值y随x的增大而减小时，x的取值范围是( )
化为一元二次方程的一般形式是__________，它的一次项系数是__________．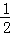
）=0，若等腰三角形ABC的一边长a=4，另一边长b、c恰好是这个方程的两个实数根，求△ABC的周长．
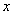的值是（ ）
D．
