题目内容
已知关于x的方程x2﹣(2k+1)x+4(k﹣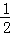 )=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
)=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
【考点】一元二次方程的应用;三角形三边关系;等腰三角形的性质.
【专题】计算题.
【分析】先利用因式分解法求出两根,再根据a=4为底边,a=4为腰,分别确定b,c的值,进而求出三角形的周长即可.
【解答】解:x2﹣(2k+1)x+4k﹣2=0,
整理得(x﹣2)[x﹣(2k﹣1)]=0,
∴x1=2,x2=2k﹣1,
当a=4为等腰△ABC的底边,则有b=c,
因为b、c恰是这个方程的两根,则2=2k﹣1,
解得k=1.5,
则三 角形的三边长分别为:2,2,4,
角形的三边长分别为:2,2,4,
∵2+2=4,这不满足三角形三边的关系,舍去;
当a=4为等腰△ABC的腰,
因为b、c恰是这个方程的两根,所以只能2k﹣1=4,
则三角形三边长分别为:2,4,4,
此时三角形的周长为2+4+4=10.
∴△ABC的周长为10.
【点评】考查一元二次方程的应用;分类探讨a=4是等腰三角形的一边的情况是解决本题的难点.

练习册系列答案
相关题目
 B=∠C D.∠BDA=∠CDA
B=∠C D.∠BDA=∠CDA
 =0的根的情况是( )
=0的根的情况是( )
 1、2、﹣15 B.1、﹣2、﹣15 C.﹣1、﹣2、﹣15 D.﹣1、2、﹣15
1、2、﹣15 B.1、﹣2、﹣15 C.﹣1、﹣2、﹣15 D.﹣1、2、﹣15 形的底和腰是方程x2﹣6x+8=0的两根,则这个三角形的周长为( )
形的底和腰是方程x2﹣6x+8=0的两根,则这个三角形的周长为( ) 与
与 合并后结果为
合并后结果为 ,则
,则